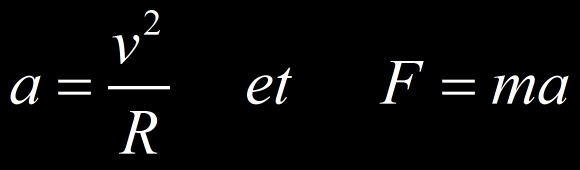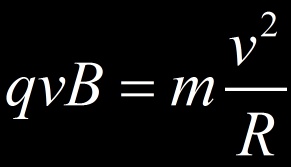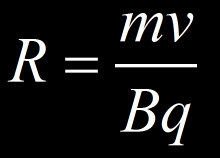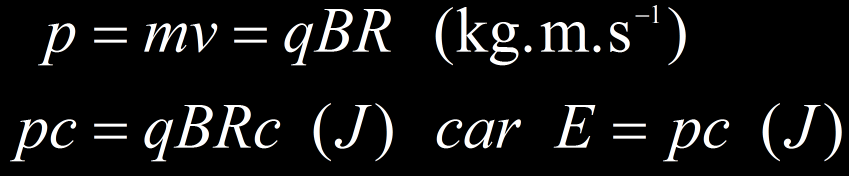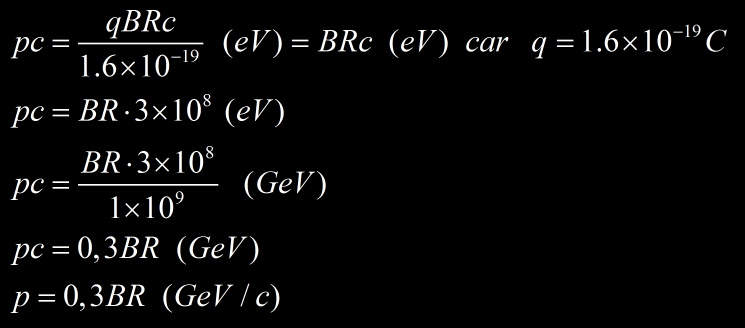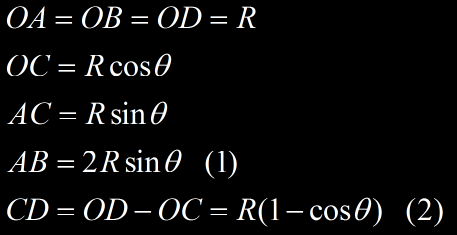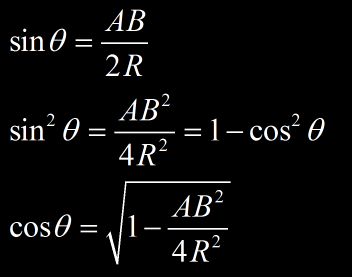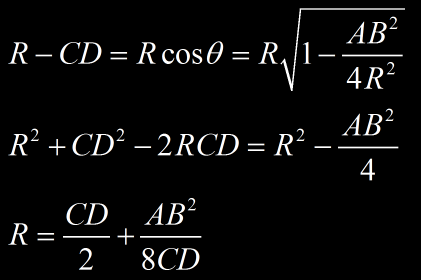A cloud chamber without magnetic field shows little interest. The Lorentz force will deflect the lightly charged particles, such as electron and positon, according to their charges (electron will deflect to left and positon to right, but this depend on the direction of magnetic field). The particles will describe « circles » where R is the radius of curvature. By mesuring R, you can rougly estimate the energy of the particle as you know it’s mass and the intensity of the magnetic field (R=mv/Bq and E=m02c4+p2c2).
The magnetic field is useful to detect the gamma annihilitation process (or pair creation). Without magnetic field, it’s impossible to say that we are looking at 2 differently charged particle (remenber that the pair creation process occurs only when the energy of the gamma is at last of 1.02 MeV, cosmic radiations will provide this energy). The next picture show what a pair creation look likes.
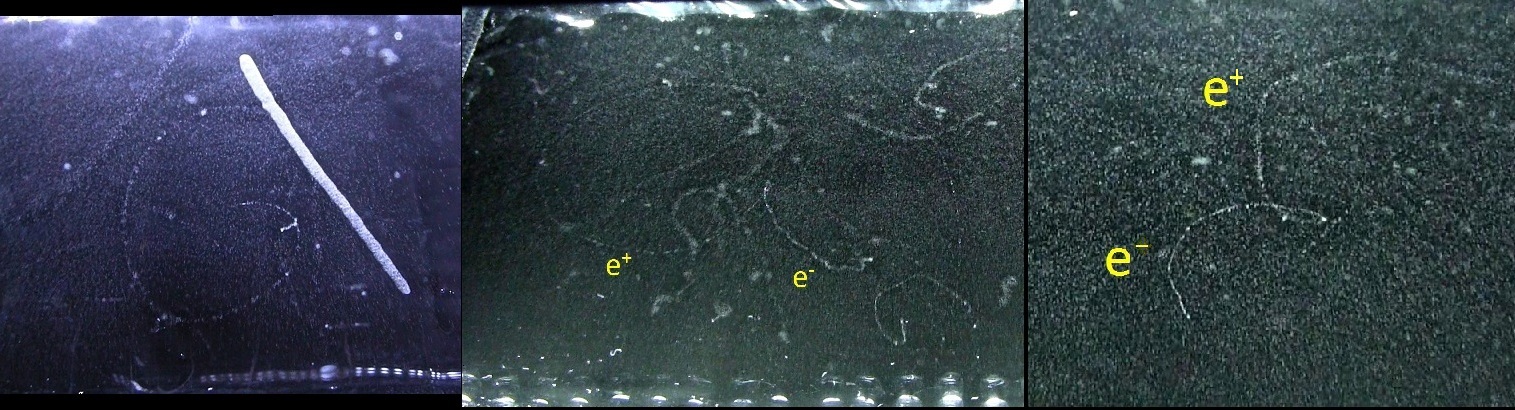
Left : an alpha particle is not subject to the magnetic field because this particle is too heavy to be deflected by the present field, but the electron is deflected (if they have energy < 1MeV which is often the case). Magnetic field can also discriminate muons from electron : Muons are 207 times heavier than electron so they are not subject to deflection (only if they have very low energy). Right : pair creation (gamma annihilation)
The magnetic field is provided in the chamber with a Neodymium magnet. Now the theory about the Lorentz force.
Lorentz Force
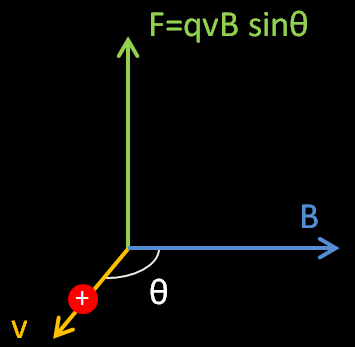
Si l’on considère un proton de charge q=+1,6×10-19 C se déplaçant dans un champ magnétique dont la direction est donnée par le vecteur vitesse B (les croix bleus indiquent que le pôle Nord s’éloigne de l’observateur), la particule subira une force perpendiculaire à la direction de son vecteur vitesse et du champ magnétique : c’est la force de Lorentz. Elle décrira une trajectoire sous la forme d’un cercle. La direction de la force centripète passe toujours au centre du cercle décrit par la particule, comme illustrée sur le schéma ci dessous.
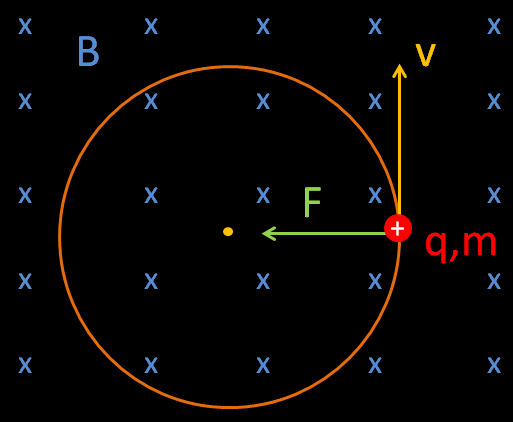
Trajectoire d’une charge positive (cercle orange) se déplaçant sous un champ magnétique
La force de Lorentz s’exprime par :
Avec θ l’angle entre la direction du vecteur vitesse et du champ magnétique .
Pour que la particule soit soumise à la force la plus intense possible, il faut que sin θ = 1 ce qui est possible si θ=90°. Dans toutes les expériences mettant en oeuvre des déviations de particules, le champ magnétique est ainsi toujours perpendiculaire à la direction de la vitesse de la particule afin d’avoir la plus grande force possible. Il convient de préciser que la force de Lorentz agit perpendiculairement à la direction de la vélocité, c’est donc une force qui ne travaille pas : un champ magnétique ne fait que dévier la trajectoire une particule, mais il ne l’accélère pas (seul un champ électrique permet d’accélérer une charge).
La direction de la force dépend du sens du vecteur champ magnétique, du sens du vecteur vitesse de la particule et de la charge de celle ci. La direction de la force se détermine à l’aide de la règle de la main droite :
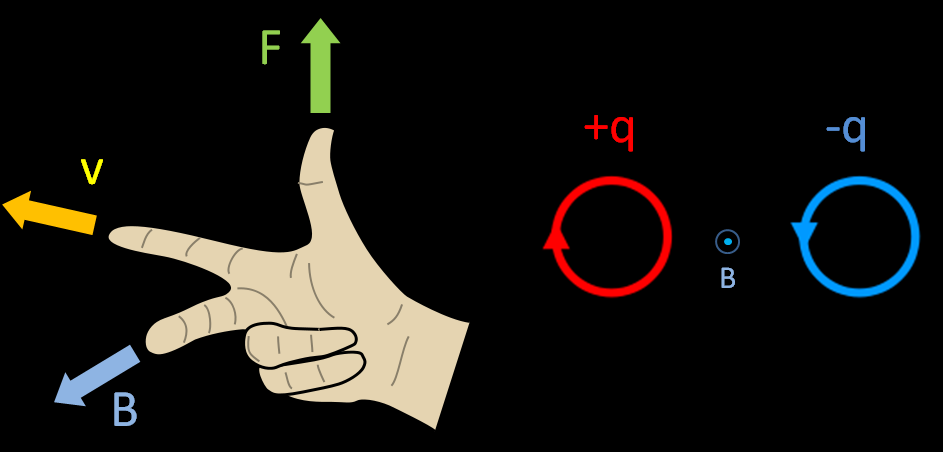
La « règle de la main droite » permet de déterminer la direction de la force de Lorentz. Le Majeure représente la direction du champ Magnétique, L’Index pour la vitesse, et le Pouce pour la force (car une force « pousse »).
Si l’on considère une charge positive (+q) se déplaçant vers le haut de l’écran, avec la direction du champ magnétique venant vers l’observateur (on observe le pole Nord d’un aimant par ex.), la particule sera déviée « vers la droite » comme le montre le cercle rouge. A l’inverse, si la particule à une charge négative (-q) comme un électron, il faut inverser le résultat précédent : la particule est déviée « vers la gauche ».
Nous avons jusqu’ici considéré que les particules faisaient des cercles sous l’action d’un champ magnétique. En réalité, le rayon de l’orbite (plus précisément le rayon du cercle osculateur) dépend de la charge, de la vélocité, de la masse de la particule et de l’intensité du champ magnétique.
Une particule soumise à une force F à effet centripète possède une accélération a qui s’exprime par :
Suivant la valeur des deux membres de l’équation, les particules décriront des rayons de courbure différent. On considère qu’une trajectoire droite à un rayon de courbure qui tend vers l’infini alors qu’un cercle à un rayon de courbure qui tend vers 0.
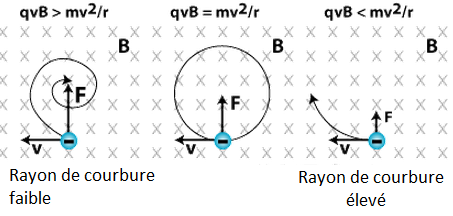
Avec m, B,q fixé, la variable de l’équation est la vitesse. Plus une particule est lente et plus sa trajectoire sera courbée (la trajectoire se rapproche d’un cercle). A l’inverse, plus une particule est rapide et plus le rayon de courbure est élevé : la trajectoire se rapproche de celle d’une droite.
On a le rayon du cercle osculateur qui s’exprime par :
A partir de cette équation, on peut remonter à l’énergie de la particule en mesurant le rayon du cercle et en connaissant la masse, la charge de la particule et l’intensité du champ magnétique.

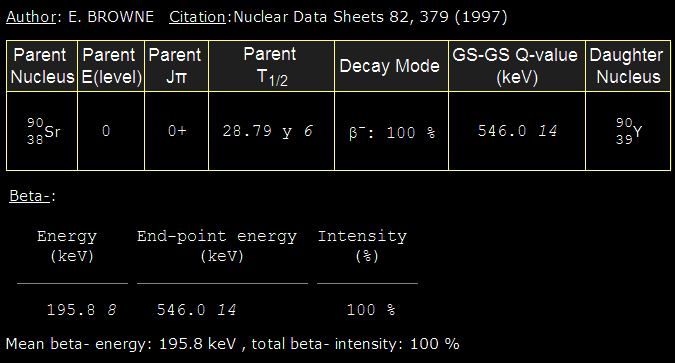
Déviation des électrons émis d’une source de Sr90 dans la chambre à brouillard thermoélectrique. Le vecteur champ magnétique est perpendiculaire au plan d’interaction et son sens est dirigé vers l’observateur. Les électrons se dirigent de bas en haut et sont donc déviés vers la gauche d’après la règle de la main droite.
A m,B,q constant, le rayon de courbure dépend essentiellement de la vitesse de la particule. Plus la particule est rapide, moins elle subit l’influence du champ magnétique et moins elle « courbe ». On peut observer cette tendance dans la chambre à brouillard, en mettant une source d’électron « émis à énergie variable » (photo ci contre). La source est ici du Strontium 90, source « bêta pure » (la désintégration du Strontium en Yttrium ne génère que des électrons). L’énergie cinétique des électrons de désintégration varie entre 0 et 546 keV (portée max dans l’air : environ 1,6 m). Le reste de l’énergie est partagée avec un anti-neutrino. On observe sur la photo que certaines trajectoires électroniques sont plus déviées que d’autre par le champ magnétique, car les vitesses des électrons sont différentes. La flèche jaune indique une trajectoire avec un rayon de courbure faible, tandis que la flèche verte montre une trajectoire avec un rayon de courbure élevé : cette dernière trajectoire correspond au passage d’un électron rapide, tandis que la trajectoire indiqué par la flèche jaune correspond au passage d’un électron plus lent.
.
Il est parfois commode d’exprimer en fonction du momentum le rayon du cercle osculateur. Le développement suivant est valable pour une particule de charge |q|=1 (électron, proton, muon…), et dans des situations relativistes ou non relativistes.
Il suffit de connaitre B et R pour obtenir la quantité de mouvement p=mv de la particule. Le momentum est exprimé en GeV/c si B est en Tesla et R en mètre. L’intensité du champ magnétique est déterminée par les conditions expérimentale (il peut s’agir d’un aimant ou d’un électroaimant) et le rayon du cercle osculateur s’obtient par mesure sur la trajectoire d’une particule.
A titre d’exemple, une particule de momentum 1 GeV/c décrit un cercle de rayon R=1,11 m dans la chambre à bulle du Fermilab (diamètre de la chambre = 4,4 m). Le champ magnétique était de 3T (images ci dessous).

Les deux photos de gauche montrent l’assemblage de l’aimant supraconducteur refroidi à Helium liquide et produisant 3T en son centre. La chambre à bulle de 4,6 m était placée à l’intérieur de l’aimant. Elle fut construite en 1973 et démantelée en 1988 après avoir photographiée 3 millions d’événements.
.
Mesure du rayon du cercle osculateur ou du « rayon de courbure R »
Lorsqu’un électron traverse un champ magnétique, sa trajectoire est courbée. Mais l’intensité du champ magnétique varie rapidement suivant la géométrie de l’expérience et donc la courbure de la trajectoire de la particule varie également. L’équation précédente permet de calculer la quantité de mouvement d’une particule en mesurant son rayon de courbure en un point donné, en traçant le cercle osculateur en ce point. Le cercle osculateur est le cercle qui « épouse la courbe le mieux possible » au point donné. Sur la figure ci dessous, W désigne le cercle osculateur au point de la trajectoire D. Le rayon R du cercle est le rayon de courbure de la courbe en D. La quantité de mouvement calculée à partir de la courbure (AB) correspondra uniquement à cette portion de trajectoire de la particule. Pour calculer la quantité de mouvement à un autre point de la trajectoire de la particule, il faudra tracer un nouveau cercle osculateur et déterminer R.
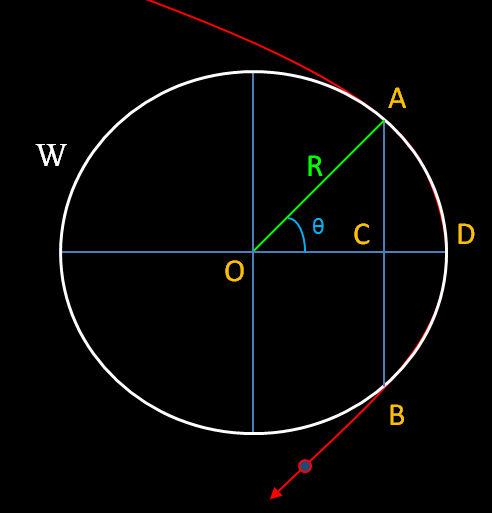
Cercle osculateur W épousant au mieux la courbure de la trajectoire (en rouge) d’une particule au point D.
Calcul du rayon de courbure R
On a :
Dans (1) :
Cas pratique : calcul de l’énergie cinétique de la particule dans la chambre à brouillard
On considère l’image ci dessous. Il s’agit de la trajectoire courbée d’un électron sous un champ magnétique, émis par une source de Sr 90. Cette expérience à été faite dans une version de chambre à brouillard plus ancienne que celle présentée sur le site. A l’époque, la surface d’interaction mesurait 12×8 cm. Peut t-on estimer l’énergie cinétique de la particule traversant la chambre ?

On peut observer deux trajectoires d’électrons. L’une est plus courbée que l’autre, ce qui indique que la particule à moins d’énergie cinétique. Le calcul portera sur l’électron dont la trajectoire est la plus courbée
Pour calculer le momentum de la particule, il faut obtenir le rayon de courbure. Ce dernier se calcule en mesurant les distances AB et CD. Pour effectuer des mesures précises de distance, il aurait fallut indiquer des marques sur la surface d’interaction comme le font les physiciens dans les chambres à bulles. Néanmoins, par construction, la longueur de référence de 4 cm est connu (elle correspond à la largeur d’un peltier). Sur la trajectoire on relève la distance AB, qui vaut ici 3,7 cm. La distance CD mesure 0,8 cm. On calcule (suivant la formule précédente) que le rayon de courbure vaut R=2,5 cm.
L’intensité du champ magnétique peut être estimée à 100 mT d’après l’aimant utilisé. Le calcul du momentum donne :
- p=0,3BR=0,3 x 0,1 x 0,025 = 0,75 MeV/c
En utilisant l’équation définit dans la page de la boite à outils relativiste, on peut calculer l’énergie cinétique de la particule, sachant qu’il s’agit d’un électron.
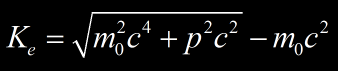 Soit Ke=(0,511²+0,75²)1/2 – 0,511 = 0,396 MeV
Soit Ke=(0,511²+0,75²)1/2 – 0,511 = 0,396 MeV
L’électron à une énergie d’environ 400 keV (aux incertitudes près !).
Le Strontium 90 émet des électrons à une énergie maximale de 546 keV. L’autre électron dont la trajectoire est moins courbée sur la photo précédente, est plus énergétique et à donc une énergie comprise entre 400 et 546 keV.
.
.
.