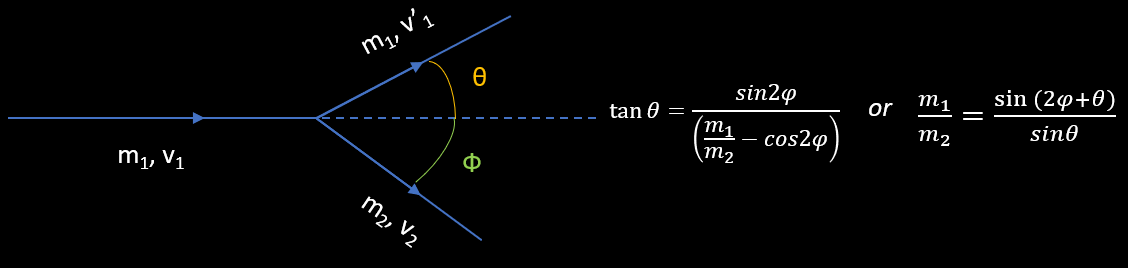
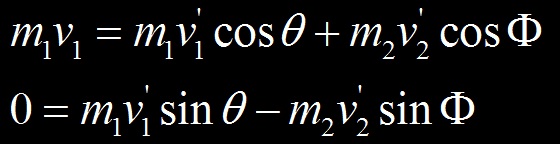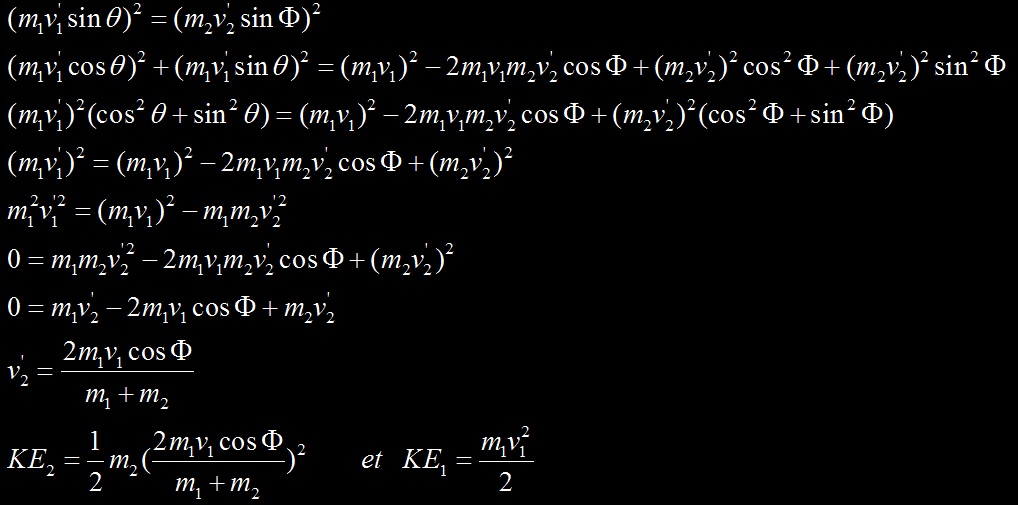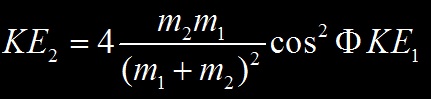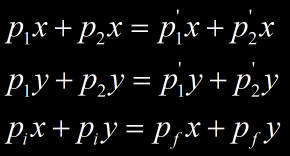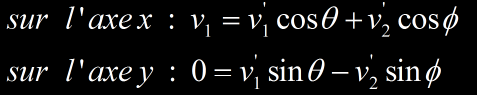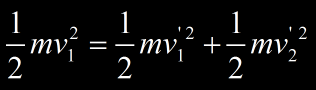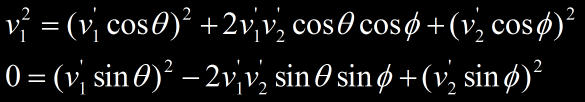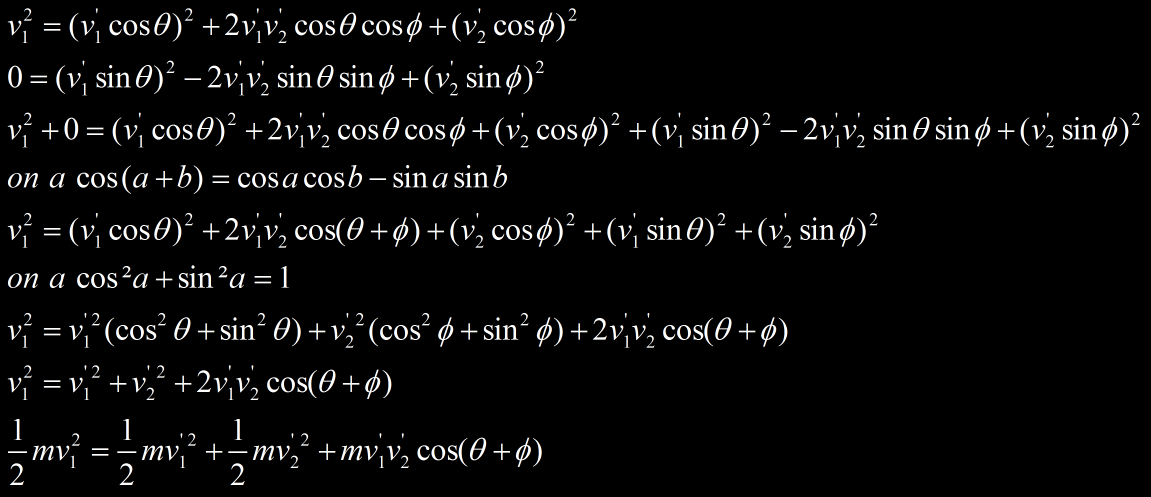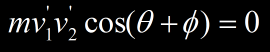Démonstration de la formule classique de collision élastique entre deux particules, dont l’une est immobile (m2).
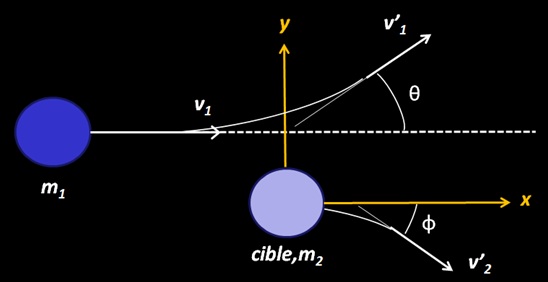
On conserve la quantité de mouvement sur les axes x et y, en projetant sur les axes suivant les angles de déviation dans l’état final :
On obtient une autre égalité en conservant l’énergie cinétique totale du système.
Le reste du développement suit, avec cos²a+sin²a=1 :
On obtient finalement l’énergie cinétique maximale transférable à la cible (m2).
Et si m1=m2 (cas d’une diffusion neutron-proton ou proton-proton par exemple),
Angle de séparation et énergie cinétique à l’issu d’ une collision élastique non frontal entre deux particules de même masse
Considérons le schéma tout en haut de la page. On a m1=m2=m. Cette démonstration à pour but de spécifier l’angle de diffusion totale (θ+Φ) entre les particules et l’énergie cinétique de celles ci après le choc.
p1x et p2x représente la quantité de mouvement de la particule 1 et 2 sur l’axe x. p’ est la quantité de mouvement après le choc. pix et piy représentent les momentum à l’état initial, et pfx et pfy les momentum à l’état final. La quantité de mouvement totale ainsi que l’énergie cinétique totale se conserve dans le cas des collisions élastiques.
En conservant la quantité de mouvement on obtient deux équations :
La conservation de l’énergie cinétique totale donne l’équation suivante :
On élève au carré les membres des équations portant sur la conservation des momentum :
On somme ces deux équations :
Or nous avons vu d’après la conservation de l’énergie cinétique que cette équation doit être respectée :
ce qui nécessite que :
Ce terme peut devenir nul si :
- v‘1 = 0 , ce qui est le cas s’il s’agit d’une collision frontale (b=0). La particule incidente s’arrête et transfert sa quantité de mouvement à la cible (cas du « carreau de pétanque »).
- v‘2 = 0, pas de collision
- cos (θ+Φ)=0 ce qui implique que l’angle de séparation entre les particules θ+Φ=90°
See also this PDF :