Cloudylabs

Particule lourdes

On peut considérer en première approximation la matière comme une soupe d’électron libre et de noyau immobile. Lorsqu’une particule chargée, par exemple un proton, va traverser cette « soupe » elle va subir l’influence des champs électrostatiques des électrons et des noyaux.

Un proton est 1836 fois plus lourd qu’un électron. On peut considérer l’analogie suivante. Le même rapport de masse existe entre une boule de bowling de 7 kg et une bille de polystyrène de 3,5 grammes. Lorsqu’on envoi la boule de bowling dans un champ de billes de polystyrène, celle ci ne déviera pas de sa trajectoire et sa vitesse sera inchangé car la masse des cibles est trop petite pour avoir une quelconque influence. Bien que l’analogie se passe avec des chocs physiques avec des masses, dans la matière les « chocs » se font à distance avec des charges via l’interaction électromagnétique.  Lorsqu’une particule chargée (autre qu’un électron !) parcours la matière, elle subira l’influence du champ électrostatique des noyaux car leur charge est bien plus importante que celle des électrons atomique : la particule sera dévié de sa trajectoire uniquement par le champ électrostatiques des noyaux. Cependant, elle interagit aussi à distance avec les électrons atomique en leur cédant de l’énergie par diffusion inélastique. Inélastique signifie qu’une partie de l’énergie cinétique est perdu lors du « choc », dans le cas  il s’agit de l’énergie de liaison des électrons atomique).

La matière ayant une structure lacunaire, ces déviations de trajectoire s’exprime avec une certaine probabilité qui dépend de nombreux paramètres comme on va le voir ci dessous.

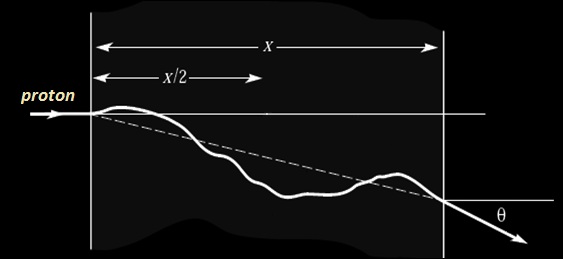
Trajectoire d’un proton traversant une épaisseur x de matière, les déviations sont exagérés par rapport à la réalité

Les diffusions successives de la particule sur les noyaux rencontrés au cours de son parcours dans la matière vont modifier sa trajectoire initial selon un angle Θ créant une trajectoire erratique. On désigne ce comportement par la « diffusion multiple Coulombienne ».  Les paramètres influant sur Θ sont exprimés dans l’équation ci dessous.

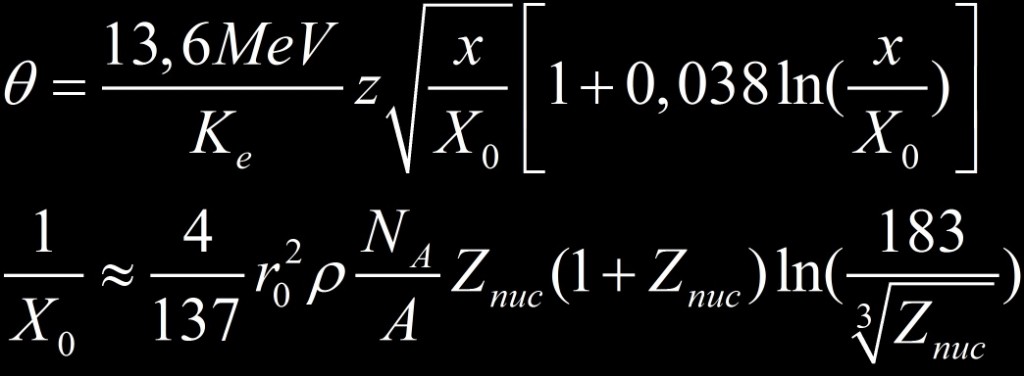
Ke = énergie cinétique de la particule, z sa charge, X0 la longueur de radiation et x l’épaisseur de matière traversée.
r₀ est le rayon de l’électron, A la masse molaire du matériau, Z_nuc la charge du matériau, N_a le nombre d’Avogadro et ρ sa masse volumique. La grandeur X₀ est explicitée ici.

Avec ces données plusieurs constatations :

• Plus l’énergie cinétique de la particule est faible et plus les déviations augmente (plus la particule est lente et plus elle subit l’influence du noyau)
• Plus la particule est chargée et plus elle subira de déviation, de même que si l’épaisseur de matière augmente.
• Par rapport à la variable X₀, plus le matériau est dense et plus les noyaux sont lourds (disposant de beaucoup de charge), et plus l’angle de déviation sera important.

Electron et positons

Nous avons considéré jusque ici des particules incidente plus lourde qu’un électron.  Dans le cas d’un électron parcourant la matière, celui ci va subir les champs électrostatiques des électrons atomiques et des noyaux. Les masses étant identiques, l’électron incident va à chaque chocs (toujours à distance) pourvoir transmettre une quantité non négligeable de son énergie aux électrons qu’il rencontre (l’analogie peut se prendre avec un « carreau » en pétanque : lors du choc, la boule initialement statique repars avec toute l’énergie cinétique !).

Contrairement aux particules lourdes, les électrons pourront diffusés sur les électrons atomiques, statistiquement plus nombreux que les noyaux.

Bremsstrahlung ou « rayonnement de freinage »

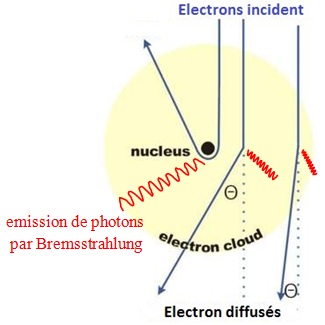
Les angles de diffusion dépendent de l’endroit où passe l’électron dans un atome. Plus les angles sont élevés et plus l’émission de rayonnement de freinage est importante.

 Lorsqu’un électron passe à proximité d’un noyau, la force d’attraction Coulombienne F s’écrit  F = Q₁Q₂ / 4πε₀r² où Q_1,Q₂ sont les charges du noyau et de l’électron, r la distance qui les sépare. A mesure que l’électron se rapproche du noyau, r diminue et F augmente et par conséquent, l’angle de diffusion.

Lorsqu’un électron diffuse sur un autre électron, les angles de diffusion seront faible car le nombre de charge Q₁Q₂ est limité. De manière générale, pour des énergies inférieures à 300 keV, les électrons feront des tracés en « zig zag » due au multiples diffusion Coulombienne sur les électrons atomique. A haute énergie, les tracés seront rectiligne, les électrons incident étant moins sensible aux champs électrostatique des électrons atomique. Cependant lorsqu’ils passeront près d’un noyau en faisant un angle de diffusion important, une quantité non négligeable d’énergie sera perdu sous forme de rayonnement de freinage (Bremsstrahlung).

Si les angles de diffusions sont important, l’accélération de la particule augmente et la quantité de photon rayonnée par la particule s’accroît (au carré de l’accélération). La puissance rayonnée P par une particule de charge q en accélération a découle de la formule de Larmor, avec P =2 q²a²/(3c³).

En Résumé

Observation dans une chambre a brouillard