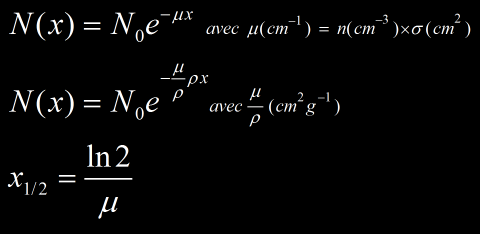Les photons n’ont pas de masse et ne sont pas chargés. Ils ne laissent donc pas de traces dans la chambre à brouillard, sauf si ils interagissent avec la matière en créant des particules chargées (électron, positon, proton…) que l’on pourra observer. Les rayonnements électromagnétiques peuvent provenir de plusieurs sources :
- lors de la désexcitation d’un noyau (rayonnement γ),
- lors de la désexcitation d’un atome (rayonnement X),
- du rayonnement de freinage des particules diffusée,
- du processus d’annihilation e–– e+,
- de la désintégration de particules neutre, notamment les pions π0.
Un rayonnement X ou γ est le même type de rayonnement. Seule la dénomination change pour distinguer les réarrangements nucléaires (γ) des réarrangements du cortège électroniques (X).
Si l’on envoi un flux de photon N0 traversant une épaisseur x de matière, on constate que le nombre de photon N ayant traversé la matière a subit une atténuation exponentielle :
Lorsqu’un photon traverse la matière, il a une certaine probabilité d’interagir par effet photoélectrique, Compton, création de paire (…) et ce avec une probabilité dépendant de la nature du matériau et de l’énergie du photon. Lorsqu’un photon à interagi, il n’est plus présent à son état originel : il à pu être absorbé où être diffusé en changeant éventuellement d’énergie. On considère l’entité N0 correspondant au nombre de photon initial avant la traversée et N le nombre de photon ayant traversé l’épaisseur de matière sans avoir interagi.
La probabilité linéique d’interaction μ (cm-1) est proportionnel au nombre de noyau par unité de volume n (cm-3) dans le matériau cible par la section efficace σ d’interaction en cm² (μ=nσ). Il est parfois plus commode d’utiliser le coefficient d’atténuation massique μ/ρ comme défini ci dessous, avec ρ la masse volumique. Lorsque N(x)=N0/2, on défini la valeur x1/2=ln2/μ . L’épaisseur de demi-atténuation x1/2 (en cm) correspond au cas où la moitié du faisceau initial du rayonnement à interagi après avoir traversé une épaisseur x1/2 (l’épaisseur de demi-atténuation joue un rôle similaire à la période T d’un élément radioactif dont la population décroit exponentiellement en fonction du temps).
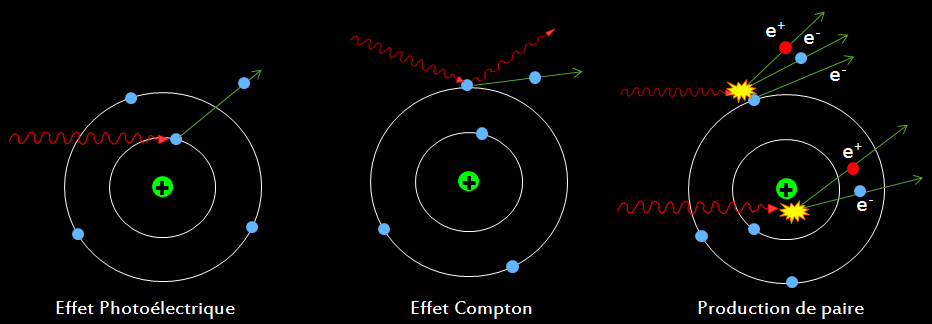
Les rayonnement électromagnétique peuvent interagir dans la matière suivant 3 processus majoritaire :
- 1) Effet photoélectrique
C’est un processus par lequel le photon incident cède toute son énergie à un électron des couches profondes qui est alors éjecté de l’atome : il y a absorption totale du photon et ionisation de l’atome. La probabilité d’interaction est d’autant plus élevée que l’électron est lié. L’énergie de l’électron est égale à l’énergie du photon incident, moins l’énergie de liaison de l’électron. L’atome réorganise ensuite son cortège électronique provoquant l’émission de rayonnement X, ou d’électrons Auger.
- 2a) Diffusion Rayleigh (ou cohérente) : le photon diffuse sur un électron atomique et change de direction, sans céder d’énergie à l’atome .
- 2b) Effet Compton (parfois dénommé diffusion incohérente)
Le photon incident cède une partie de son énergie à un électron des couches périphériques de l’atome, qui est éjecté. Il apparaît un nouveau photon diffusé, d’énergie inférieure. Il y a donc diffusion du photon incident et ionisation de l’atome. L’énergie du photon diffusé est fonction de l’angle de diffusion.
- 3) La création de paires (and triplets)
Un photon est capable de se matérialiser en une paire électron-positon hν →β++β–. Cette matérialisation ne se peut se produire que dans le champ d’une particule chargée. Si cette particule est un noyau, l’énergie du photon est transmise sous forme d’énergie cinétique à la paire électron-positon crée. Pour conserver la quantité de mouvement, le noyau recule mais du fait de sa grande masse ne reçoit quasiment aucune énergie dans le processus. L’énergie se partage inégalement entre le positon et l’électron, la somme de leur énergie étant quasi égale à celle du photon. Dans le champ coulombien d’un noyau, l’énergie seuil pour la matérialisation du photon est de 1,02 MeV. A cette énergie seuil les leptons crées ne disposent pas d’énergie cinétique (1,02 MeV correspondant à 2me). The probability of pair production is proportional to Z², where Z is the nuclear charge.
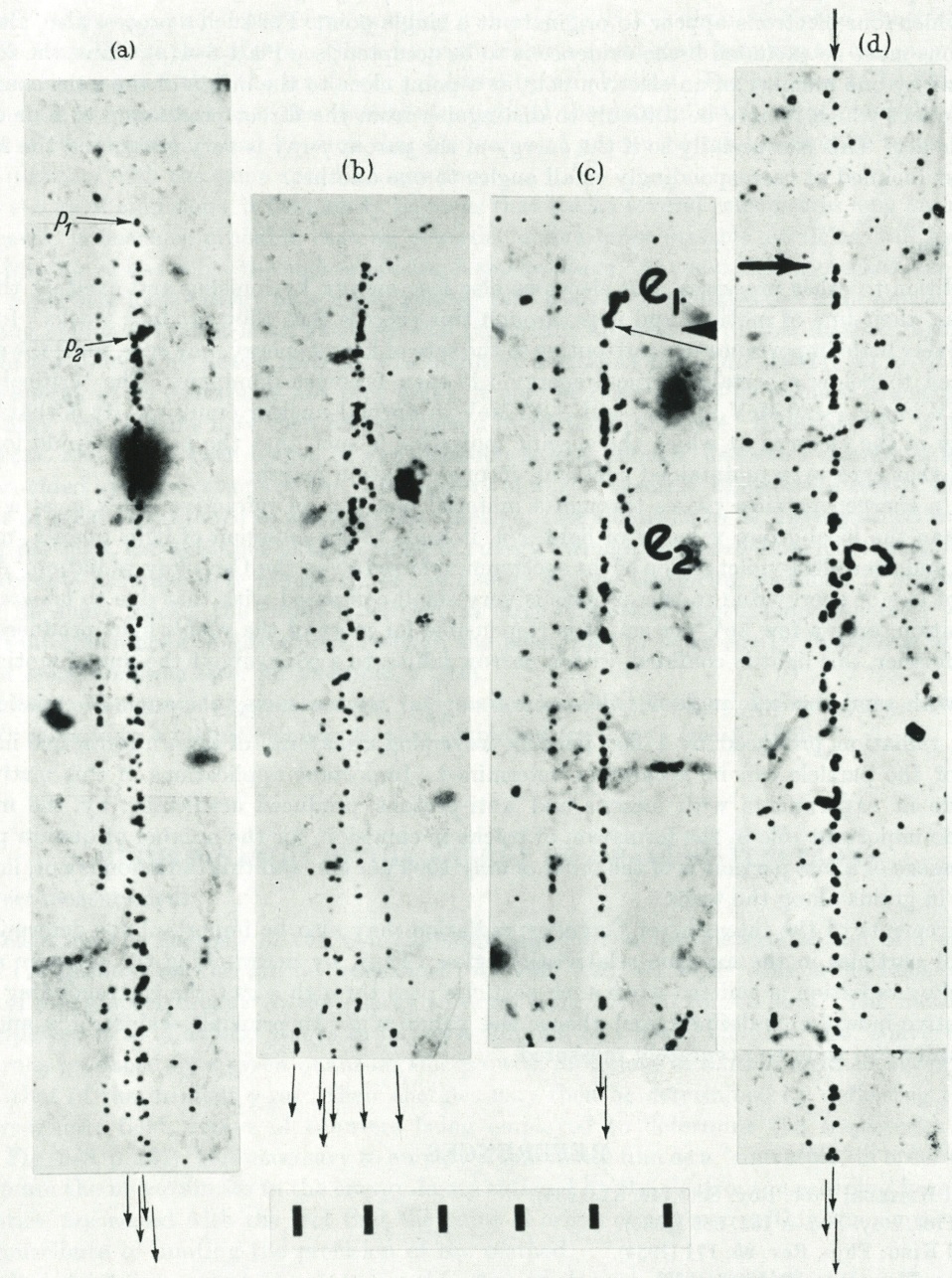
Left picture (1952) : (a) At first sight this event appears to correspond to the creation of four electrons in a single act. Closer inspection however, shows that there are two separate points (P1,P2) from each of which two electron diverge. Point P1 is a materialization of a photon. At P2, another photon materialize. This photon may come from the bremsstrahlung of one of the first pair of lepton created at point P1. Indeed, we said that high energy electron which expect bremsstrahlung emit photon with very small angular divergence between the direction of motion of the incident electron. A left, there is a single parallel track due to an associated fast electron.
(b) Creation of six singly charged particles. The relatively large angular divergence, in comparison with the energy, indicates that the tracks are not due to electrons. The event is attributed to the collision of an energetic neutron with a nucleus, and the creation of pion or heavier particles without any visible evidence for nuclear disintegration.
(c) Pair production by a photon in which two slow electrons appear to be emitted from the same centre. It appears reasonable to assume that they come from the same atom as that involved in the conversion of the photon, possibly through ionisation and the Auger effect.
(d) A pair of electrons is created at a point shown by the arrow, indistinguishable from the track of an incoming electron. The directions of motion are so nearly parallel that the tracks do not separate for several hundred microns. In individual events of this type, the origin of a pair, whether due to conversion of a photon from bremsstrahlung or to trident production, cannot be stated by confidence.
Le processus de création de paire peut aussi avoir lieu dans le champ coulombien d’un électron bien que cela soit beaucoup moins probable. On désigne souvent cette interaction par la production de ‘triplet‘. Etant donné la faible masse de l’électron ‘hôte’, celui ci reçoit une quantité de mouvement non négligeable ce qui lui permet de s’échapper de l’attraction de l’atome. L’énergie du photon se partage entre les 3 particules, l’électron ‘hôte’ et la paire électron-positon crée. L’énergie seuil pour la création de triplet est de 2.044 MeV où 1.02 MeV est converti en masse (création de la paire sans énergie cinétique). Le processus de création de triplet dans le champ d’un électron est beaucoup plus rare que la création de paire. Dans le plomb pour un γ de 5 MeV, il y a une création de triplet pour 100 créations de paires dans le champ d’un noyau.
L’existence du positon à été prédit théoriquement par Dirac en 1931 et la particule fût mis en évidence par Anderson en 1932 dans une chambre à brouillard (bien que Skobeltsyn ait déjà noté en 1929 que parmi des particules du rayonnement cosmiques, certaines se comportaient comme des électrons mais étaient déviées dans un sens contraire sous un champ magnétique). En 1933 Blacket et Occhialini confirmèrent avec leur chambre à brouillard l’existence du positon et découvrirent le phénomène des cascades électromagnétiques provenant des processus de création de paires.
La courbe suivante illustre l’importance des différents types d’interaction du photon en fonction de son énergie. L’ordonnée correspond à la section efficace σ exprimée en barn (1 barn= 10-24 cm2 ).
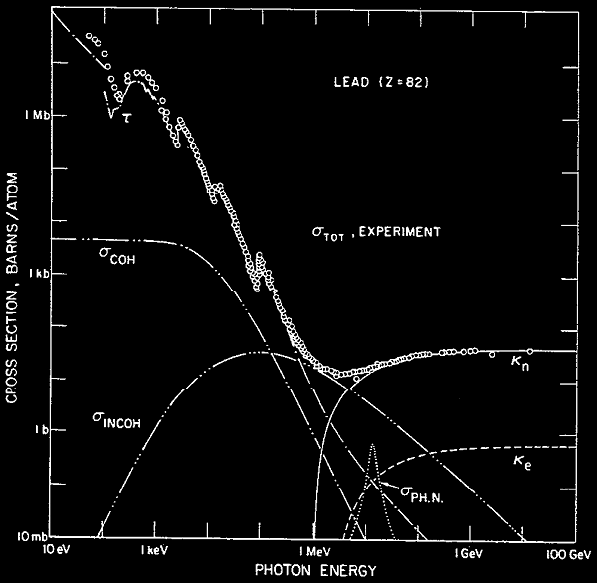
Contribution de l’effet photoélectrique τ, de la diffusion Rayleigh σcoh, de la diffusion Compton σincoh , de la production de paire dans le champ d’un noyau κn , de la production de paire dans le champ d’un électron κe , et des interactions photonucléaire σPH.N (see end of this page) , à la section efficace totale mesurée σtot dans le plomb pour des énergies de photons de 10 eV à 100 GeV. Les points mesuré σtot proviennent de 121 références.
A basse énergie (< 1 MeV) l’effet photoélectrique est le processus dominant. Dans les chambres à brouillard, les photons émis par les désintégrations des minéraux uranifère ou par la plupart des sources radioactive sont inférieur à 1 MeV. Le rayonnement cosmique au niveau de la mer est composé de rayonnement gamma ayant des énergies jusqu’à plusieurs centaines de MeV. Il reste alors possible d’observer par ordre de probabilité une paire, éventuellement un triplet ou encore et mais plus rarement une réaction photo nucléaire dans le gaz de la chambre (cf courbes d’interactions ci dessous).
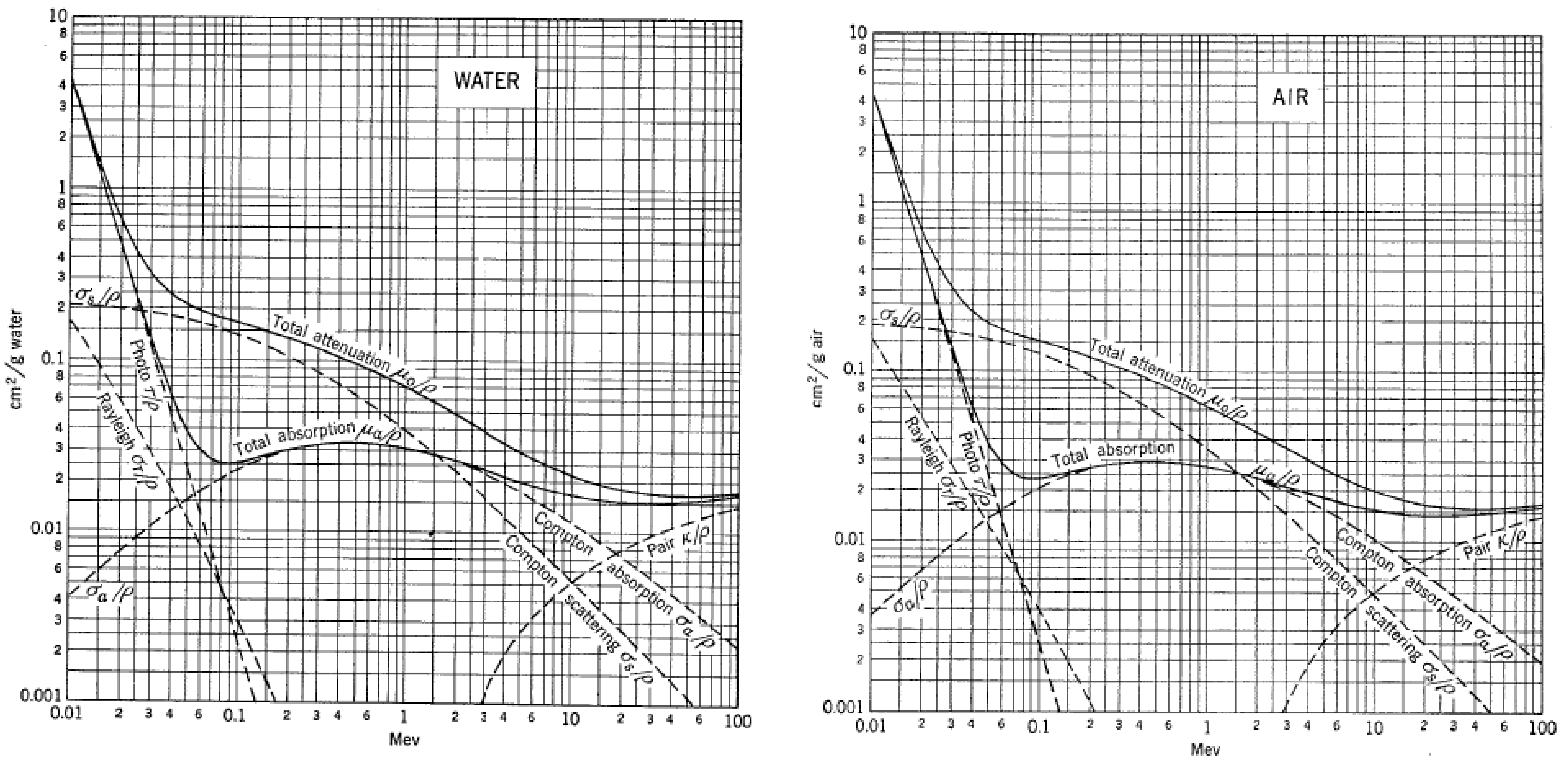
On peut préciser que la densité du matériau n’a que peu d’effet sur les probabilités d’occurrences des interactions. Exemple avec l’eau (d=1) et l’air (d=0,0012) :
About the triplet creation
When a gamma have 10 MeV of energy, the triplet interaction in air is 13 less probable than the pair creation effect. It’s thus possible to observe a triplet in a cloud chamber near sea level because gamma can still have energy of several dozen of MeV.
Back to the gamma cross section interaction curves
Les courbes de probabilité d’interactions sont exprimées souvent par le coefficient d’atténuation massique μ (cm²/g)=10-24(NA/A) σ(barn), où l’on reconnait le nombre d’Avogadro NA et le numéro atomique de l’élément. Le coefficient massique d’interaction μ est un coefficient global qui prend en compte les interactions des photons dans la matière sans préciser la nature de l’interaction ; ce coefficient global d’interaction est la somme des coefficients d’interaction respectifs des trois effets photoélectrique, Compton et création de paires (il s’agit de la courbe « total atténuation » ci dessus, à ne pas confondre avec la courbe « total absorption » qui est relié à d’autres concepts)
On peut retrouver toutes les courbes d’atténuation massiques sur le programme XCOM du National Institute of Standards and Technology.
Exemple d’application :
Quel est la portée dans l’air et dans le plomb, d’un flux de photon de 1 MeV ?
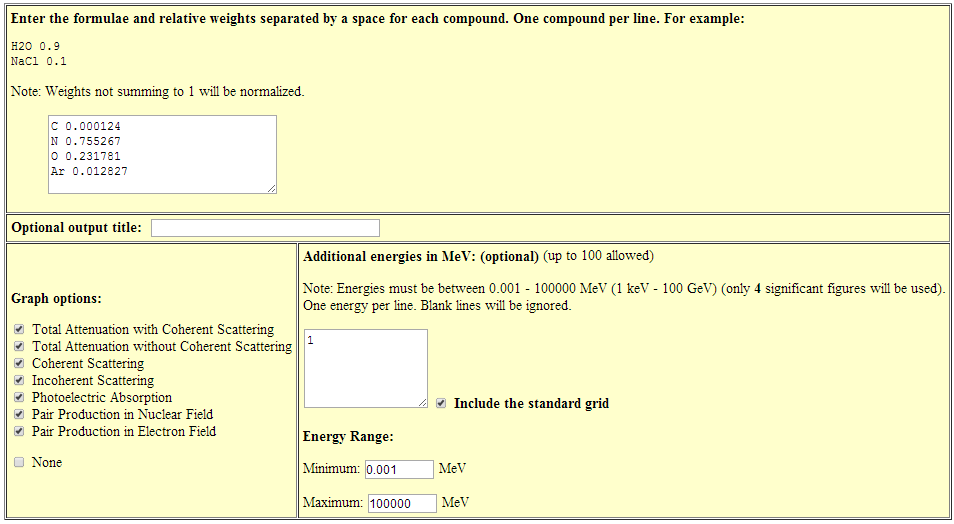
La composition de l’air est accessible ici . On se rend sur la base de donnée du NIST et on entre la composition de l’air :
Note : plus rapide => http://physics.nist.gov/PhysRefData/XrayMassCoef/tab4.html où l’air et 47 autres substances qui ont de l’intérêt pour la radioprotection sont déjà référencée.
On sélectionne toutes les options du graph et on spécifie une énergie de 1 MeV.
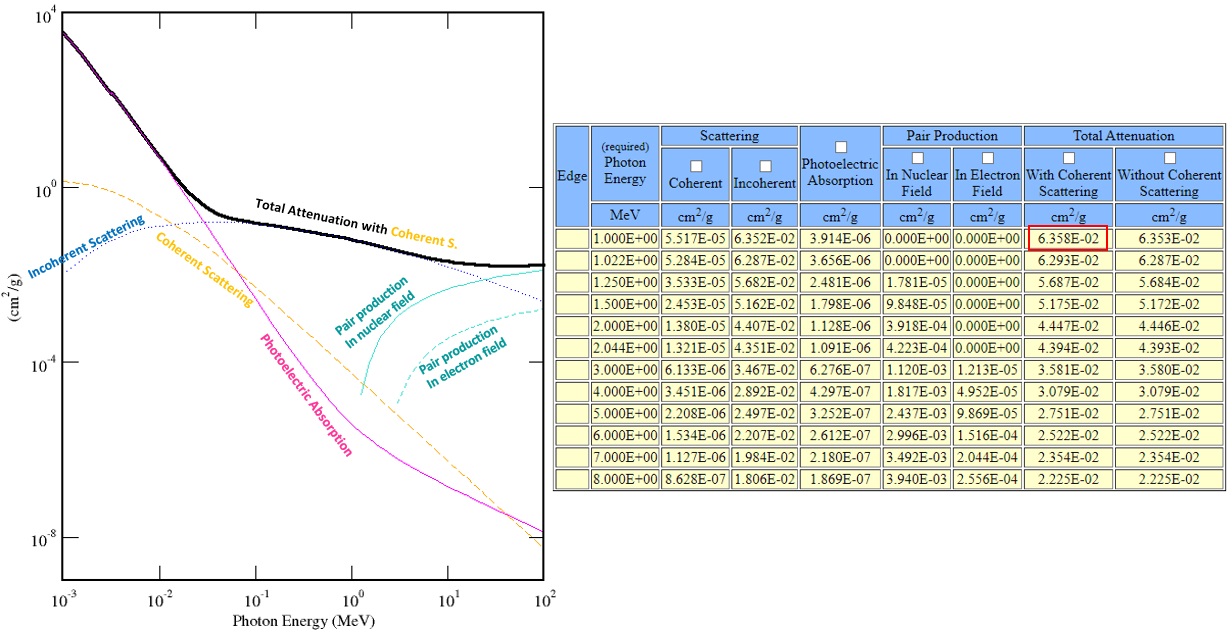
Dans l’air, la probabilité d’interaction d’un photon par création de paire dans le champ d’un noyau est très peu probable à l’énergie seuil (1,78×10-5 cm²/g). Dans le plomb : 3,8×10-4 cm²/g (très faible influence de la densité du matériau sur les probabilités d’interaction). Dans le cas de la production de triplet dans l’air à 3 MeV , l’effet est 100 fois moins probable que la création de paires, à 10 MeV, 13 fois moins probable, à 50 MeV, 8 fois moins probable , à 400 MeV, 7 fois moins probable.
On obtient la courbe d’atténuation en énergie des photons avec toutes les contributions des interactions « With coherent scattering » .
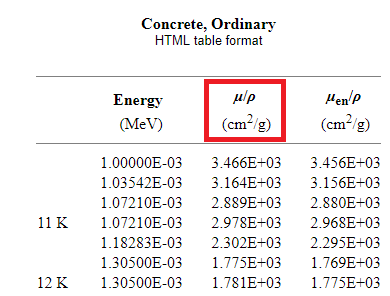
A 1 MeV, la valeur du coefficient d’atténuation massique : est de μ/ρ = 6,358 x10-2 cm²/g. Le coefficient d’atténuation linéique s’obtient en prenant en compte la densité du milieu, avec ρair = 1,20479×10-3 g/cm3 soit μ=μ/ρ x ρ =7,66 x 10-5 cm-1
On calcul l’épaisseur de demi-atténuation : x1/2=ln2/ μ = 0,693/7,66 x 10-5 = 9048 cm soit 90,4 m.
Un flux de photon de 1 MeV est atténué de moitié après un parcours de 90 mètres dans l’air (il ne reste que 50% de photon à 1 MeV après la traversée, les autres ayant interagi)
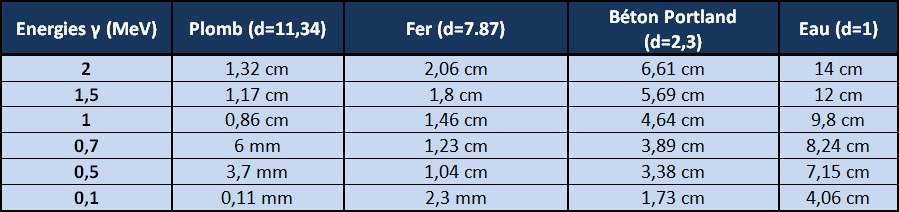
Dans le plomb à 1 MeV, x1/2=8,6 mm (de manière générale, plus le matériau est dense et plus l’atténuation des rayonnements électromagnétique est efficace).
x1/2 for common materials and energy. Exemple of calcul
Nota : dans les table du NIST il faut sélectionner la valeur du coefficient d’atténuation massique μ et non pas μen qui est le coefficient d’absorption massique en énergie prenant en compte les énergies cinétiques communiquée aux particules secondaires. Ces grandeurs ont de plus les mêmes unités.
Other process of interaction : Photodisintegration
A photonuclear reaction or a photodisintegration is a nuclear reaction induced by a photon. These reactions occur when atomic nuclei are excited via the capture of incident photons and relax by emitting one or several elementary particles, nuclei fragments or through fission.
The type of particle emitted from the excited nucleus after photo absorption greatly depends on the mass number of element. In one word, proton emission dominates for light nuclei.
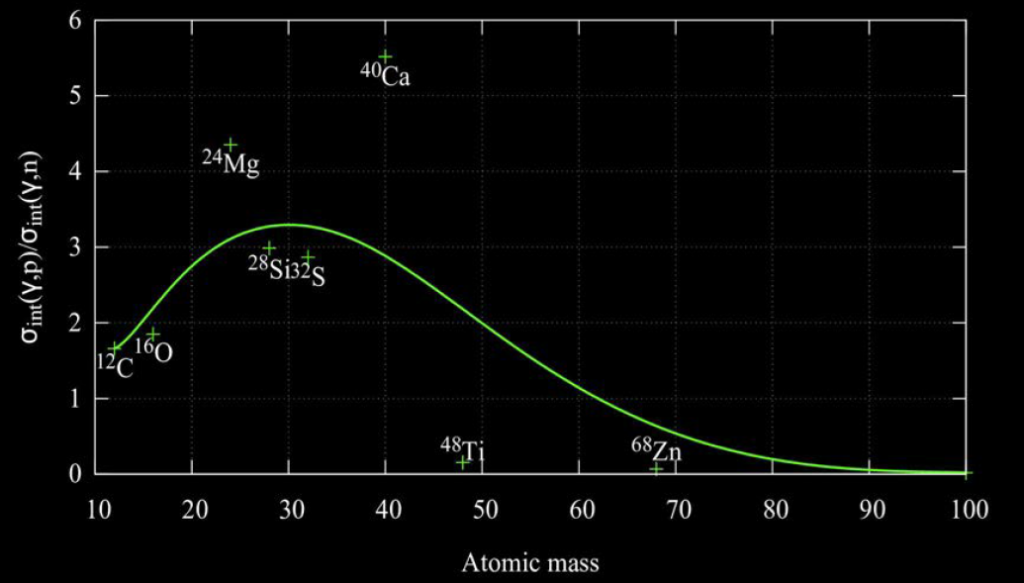
Ratio of the integral cross-sections of (γ, p) and (γ, n) reactions for 10 < A < 100 from IAEA.
Light nuclei typically have relatively low binding energies. The energy required to remove a proton or a deuteron (a proton-neutron pair) from a light nucleus is often lower compared to removing a neutron. This makes the emission of charged particles like protons or deuterons more likely. The Coulomb repulsion between proton lowers the net binding energy of each proton because part of the attractive nuclear force is counteracted by the repulsion.
Moerevoer, the height of the Coulomb barrier depends on the charge of the nucleus (Z) and the distance at which the proton is considered to be emitted. So for light nuclei the energy provided by the absorbed gamma ray is enough to allow the proton to escape the Coulomb potential, making proton emission more probable over neutrons.
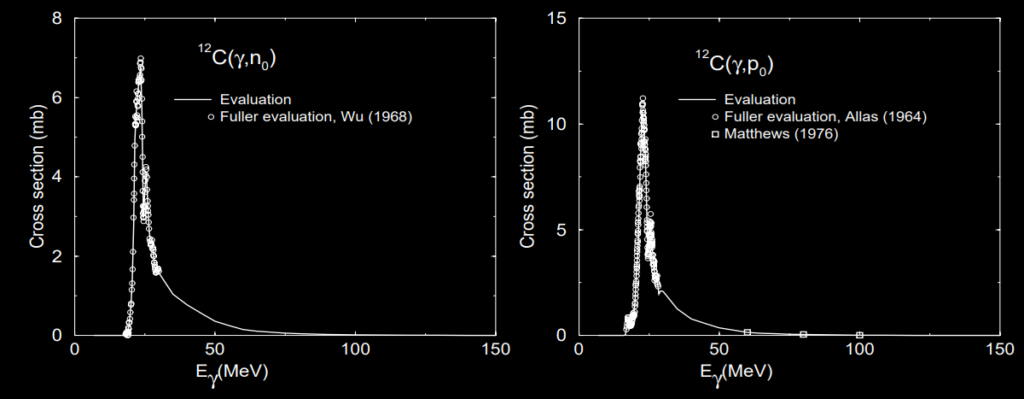
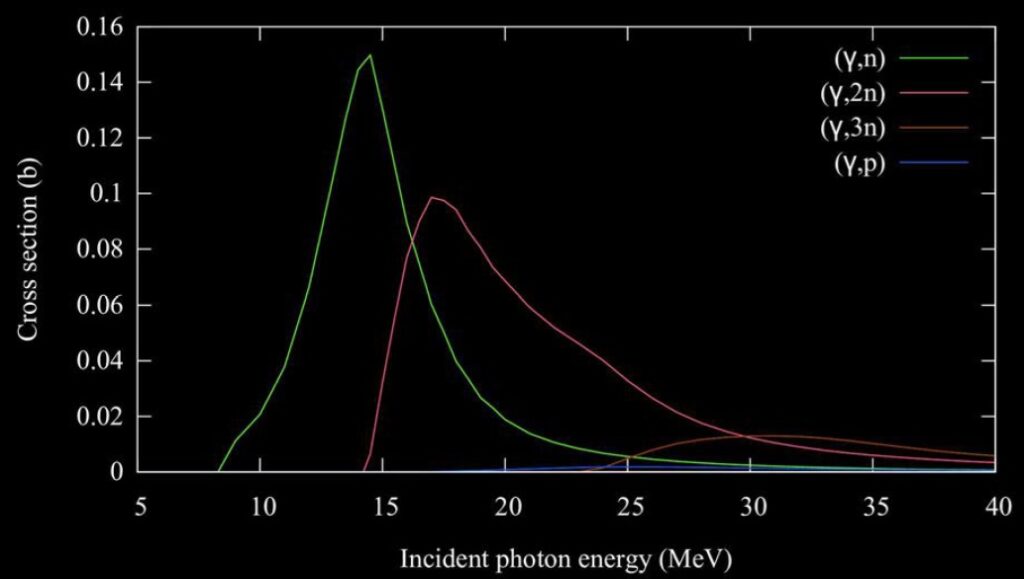
Photodisintegration cross section of 12C. For light element the emission of charged particle is more probable than the (γ, n) reactions. From IAEA.
Photodisintegration process can be classified into 3 main region :
- When the energy is low (few MeV), below a certain threshold of energy, the nucleus can absorb a gamma ray and become excited. It then go back to the fundamental state emitting gamma (example with the Mössbauer effect) or thought other process like electron capture or internal conversion (for very low energy < 1MeV).
- When the energy of the gamma reach a certain threshold (about 7-8 MeV), there is a probability that the absorption will lead to a strong excited state which will force the nucleus to emit particles or fragments : n, p, α, deuton, triton, He-3.. (this region is called the GDR Giant Dipole Resonance”).
- For energy of > 140 MeV (photomesonic region), other particles can be created. Muons can be produced in pair during the interaction of a γ-ray with the Coulomb field of a nucleus. Pions π can be photo-produced with the following reaction γ + n → π–+ p and γ + p → π0+ p.
For the case 2) it mean that a 7,16 MeV gamma can interact with an oxygen nucleus and give the reaction : γ+16O→12C+α. Several particle can be emitted. Photons with energy higher than the separation energy of two nucleons (typically above 16 MeV) can initiate (γ, 2n), (γ, pn) or (γ, 2p) reactions. For incident photon energy above 24 MeV, photonuclear reaction channels with three output particles open up: (γ,3n), (γ, 2np), etc. Autres exemples de réactions de photo-désintégration.
In a cloud chamber, we are interested with the most abundant element in air, so Oxygen and Nitrogen :
Note : despite that α particle are charged 2+ so faces a higher Coulomb barrier to leave the nucleus than proton, some nuclei have a tendency to form alpha particle clusters. In such nuclei, the emission of alpha particles can be more likely (notably in 8Be, 12C, 16O). So o other reaction are available like γ+16O→ 4 α. In this reaction, the energy threshold is only 14,44 MeV.
De l’azote 14 irradié sous des γ de 100 MeV se désintègre en un proton, un neutron et 3 particules alpha, créant une star à 4 branches dans le gaz d’une chambre à brouillard (exemple).
Le rayonnement naturel dans la chambre à brouillard where it comes indirectly from the cosmic radiation, offer sometimes some photodisintegration events (about 2 per hours at low altitude) :

The length of the picture is 40 cm wide and 20 cm high. It was taken during the recording of 1 hour of cosmic ray, and 2 events like this appeared. There is no incoming particle which would have strike a nucleus, the tracks are produced from the same point. The brightness and the length of the tracks exclude, to me, the presence of α particles. Likely 2 protons are emitted at left. Maybe the rest are deuton/triton. Some fragments don’t have a lot of kinetic energy as their path are not perfectly straight as they undergo multiple scattering.