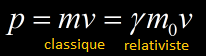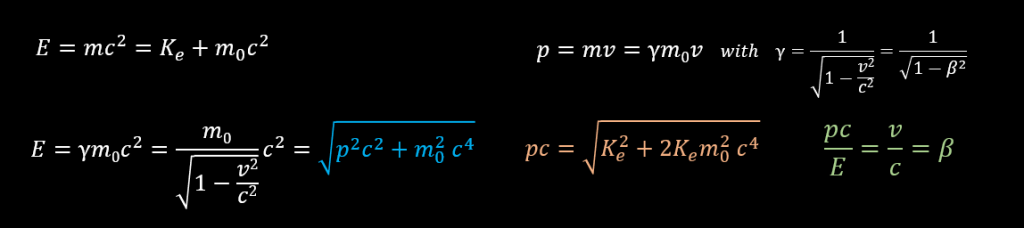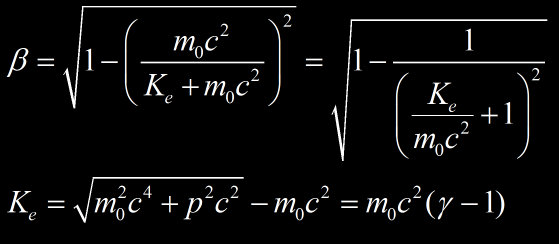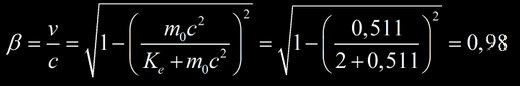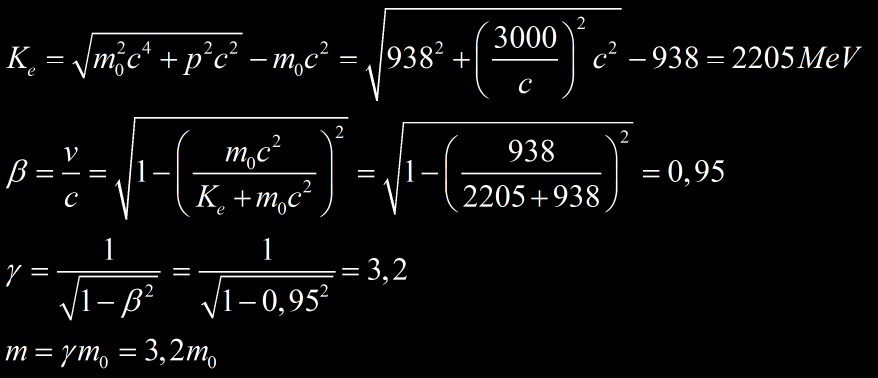Lorsque la vitesse d’une particule approche celle de la lumière, il faut prendre en compte les effets relativistes. Mais à partir de quel énergie cinétique une particule peut être considérée comme relativiste ?
On peut considérer une limite raisonnable où les résultats donnée par les équations classiques et les équations relativistes différent de 1%.
La quantité de mouvement relativiste diffère de 1% de l’expression de la quantité de mouvement classique lorsque γ=0,01 (voir la signification de cette quantité dans la suite de la page).
En injectant γ=0,01 dans l’expression de γ, on trouve que v=0,14c soit v=42 000 km/s.
Lorsqu’une particule se déplace à plus de 42 000 km/s, les calculs classiques donnent une erreur de 1% par rapport aux calculs relativistes. A v=0,41c (125 000 km/s) l’erreur est de 10%.
A partir de l’équation relativiste Ke=m0c2(γ-1) on peut calculer pour différentes particules à partir de quel énergie cinétique correspond une erreur de 1% :
- pour un électron, Ke=0,511 x (1,01-1)= 5,11 keV
- pour un muon, Ke=105,6 x (1,01-1)= 1 MeV
- pour un proton, Ke=938 x (1,01-1)= 9,38 MeV
- pour un alpha, Ke=3727 x (1,01-1)= 37 MeV
Dans une chambre à brouillard, il est commun d’observer des électrons, muons et proton avec des énergies 10 à 100 fois plus élevée que les énergies seuil précédemment calculée. Ainsi il faudra utiliser systématiquement les expressions relativistes pour ces particules.
Les particules alpha issus des réactions de désintégration que l’on observe dans la chambre à brouillard ne sont émises qu’avec des énergies maximum de 10 MeV, énergie bien en dessous de l’énergie seuil où l’on doit prendre en compte les effets relativistes. L’énergie cinétique d’une particule alpha pourra s’exprimer simplement par l’équation classique Ke=0,5mv² et la quantité de mouvement par p=mv. Les deux quantités sont reliés classiquement par Ke=p²/(2m).
Les formules suivantes sont valables pour des vitesses relativistes et permettent de calculer la quantité de mouvement p, l’énergie cinétique Ke , la vitesse d’une particule ou le facteur de Lorentz γ. La vitesse de la lumière est exprimée par c. Note that m0 is the mass of the particle at rest (with no kinetic energy, it’s a constant). As energy and mass can be converted each other by c², there are the « same quantity ». E represent all the energy of the particle : it’s kinetic energy + it’s rest mass. Next, some useful relativist quantity, specially the colored equations.
We can rearrange the above equations to obtain also :
L’énergie totale d’une particule est la somme de son énergie cinétique et de son énergie de masse « au repos ». D’après la théorie de la relativité d’Einstein (1905), la masse d’un objet augmente avec sa vélocité, par rapport à l’observateur. Lorsque l’énergie cinétique de l’objet est égale à 0, la masse (inertielle) de celui-ci est la masse « au repos » m0 avec laquelle nous sommes familiarisée. Pour des vitesses bien inférieur à celle de la lumière, l’augmentation de masse inertielle est imperceptible pour l’observateur, mais si la vitesse lumière est approchée, l’augmentation est très rapide et théoriquement jusque vers l’infini.
La masse au repos de quelques particules sont donnés ci dessous.
Pour convertir des kg en MeV/c² on a E=m0c² avec E en joules. On défini l’électronvolt avec 1 eV= 1,6×10-19 J et 1 MeV = 1,6×10-13 J. Dans le cas du proton, l’énergie de masse de la particule vaut E(J)=1,67×10-27 kg x (3×108)2=1,503×10-10 J=1,503×10-10 / 1,6×10-13 MeV=938,2 MeV. Avec E=m0c², la masse du proton vaut donc m0=E/c²=938,2/c²=938,2 MeV/c².
Exemples d’application :
Quel est la vitesse d’un électron ayant une énergie cinétique de 2 MeV ?
En utilisant l’équation précédente avec des données en MeV :
La vitesse d’un électron de 2 MeV dans le vide est de v=0,98c (98% de la vitesse lumière)
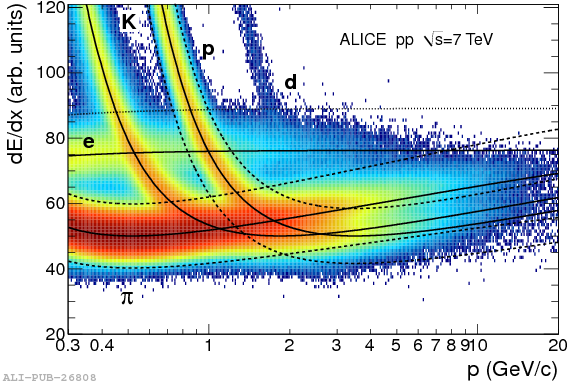
La courbe ci dessous montre la perte d’énergie collisionnel d’électron, de pion, de kaon, de proton et de deutéron dans le gaz de la Time Projection Chamber d’ALICE au LHC. Un proton perd le minimum d’énergie lorsque son momentum dépasse les 3 GeV/c (3000 MeV/c). A quel vitesse cela correspond t-il ? quel est la masse du proton à cette vitesse ?
Un proton de momentum 3 GeV/c à une énergie cinétique de 2,2 GeV ce qui correspond à v=0,95c. A cette vitesse, la masse inertielle du proton est 3,2 fois plus importante qu’un proton statique. Cette feuille de calcul permet d’effectuer automatiquement les conversions de ces grandeurs entre elles.
Masse relativiste
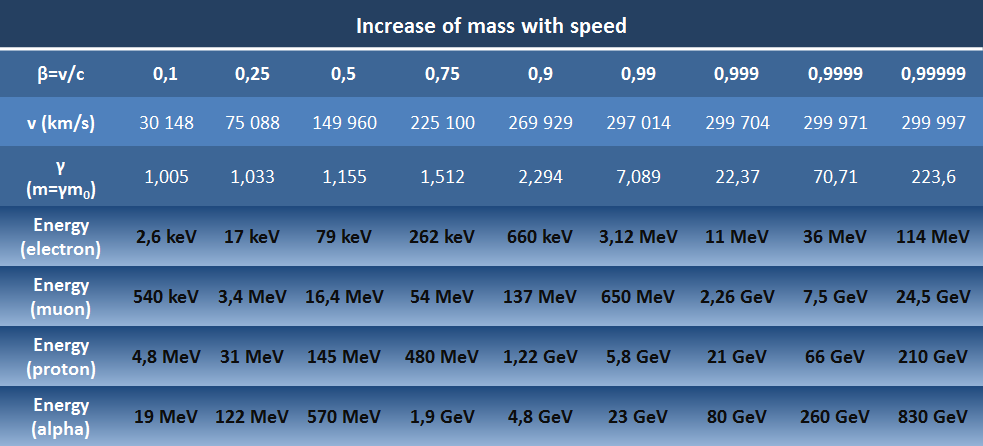
La théorie d’Einstein sur la relativité montre qu’un objet approchant la vitesse lumière voit sa masse inertielle devenir de plus en plus importante selon m=γm0. Ce concept de masse relativiste s’observe dans les chambres à brouillard lorsque par exemple des électrons relativiste (à v=0.9c, ils sont quasiment deux fois plus lourd que la masse au repos), collisionnent avec des électrons atomiques de masse m0 : l’angle entre les deux particules est inférieur à 90° alors qu’il serait droit si les particules avaient strictement la même masse intertielle. Les cyclotrons, accélérant des particules suivant une spirale jusqu’à plusieurs centaine de MeV, sont confrontés à cette augmentation de masse (pour v=0,999c, la masse de la particule s’accroît d’un facteur 22,3 !). Pour garder les particules dans le faisceau, il faut recourir à plusieurs astuces technologiques (modification du champ magnétique ou de la fréquence du champ électrique) pour compenser les effets relativistes.
‘Energy’ in the table mean ‘kinetic energy’.