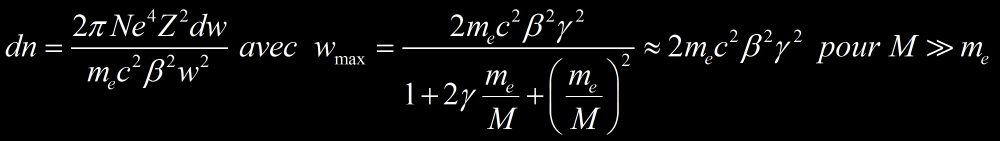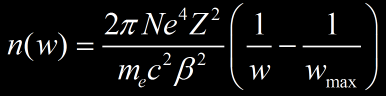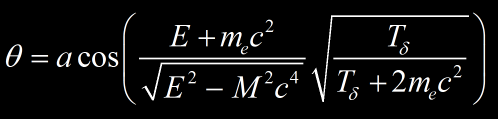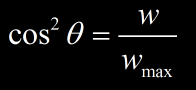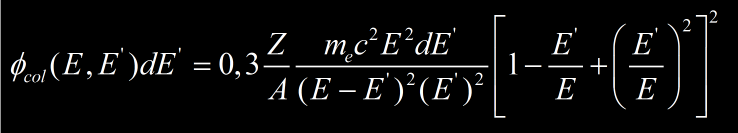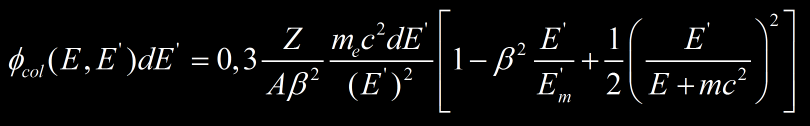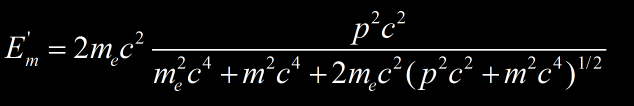Nombre de delta ray crée par unité de longueur
La formule suivante indique le nombre dn de delta ray ayant une énergie entre w et w+dw produit par unité de longueur par un ion se déplaçant à la vitesse β=v/c dans un milieu de densité électronique N. Z est la charge effective de l’ion (pour un alpha, Z= 2e à 3 MeV, Z diminue avec l’énergie de la particule comme précisé ici), e la charge de l’électron et me sa masse.
On constate d’après la formule ci dessus que plus l’énergie du delta ray est élevée (jusqu’à wmax) et plus le nombre produit de delta ray est faible. wmax est l’énergie cinétique maximale transférable à un électron lors d’une collision frontale décrit ici, mais en considérant des vitesses relativiste (si on fait tendre γ vers 1 lorsque v<<c, on trouve wmax = 2mev² en approximation).
La relation montre une dépendance en 1/v² (car β=v/c) : plus une particule est rapide et plus le nombre produit de delta ray est faible.
Un électron (delta ray) d’énergie cinétique Tδ est éjecté à un angle θ de la trajectoire de la particule incidente de masse M par l’expression :
ou par l‘expression :
Si l’on considère un delta ray d’énergie wmax , cos² θ = 1 donc θ=0°. Les delta rays les moins énergétique seront produits à des angles proche de 90° de la trajectoire de la particule incidente.
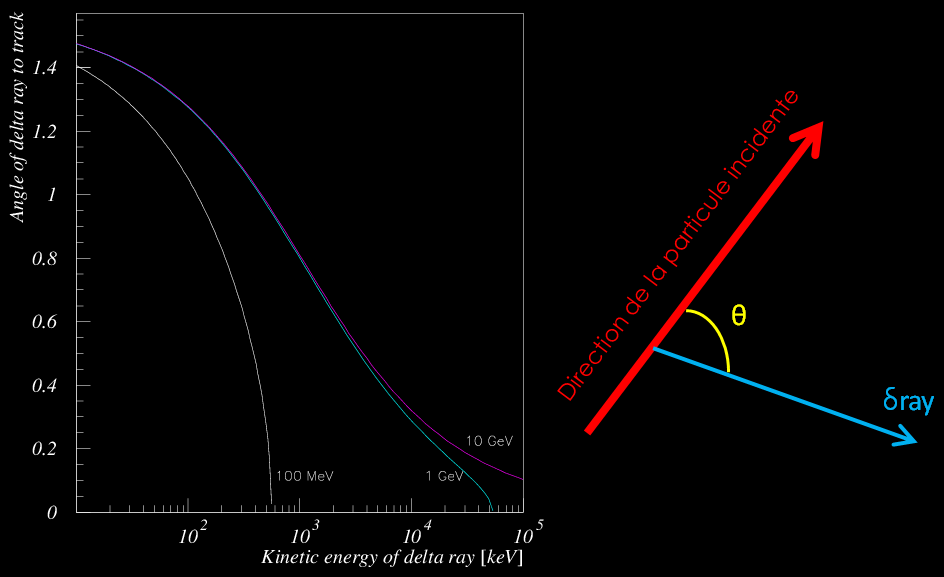
Angle d’émission de delta ray en fonction de leur énergie cinétique, éjectés par des pions de 0,1, 1 et 10 GeV, calculé à partir de la formule précédente. Les delta ray les plus probable sont ceux de moindre énergies et sont émis à des angles proches de 90°. L’ordonnée est en radian (1,57 rad = π/2)
Dans les plaques photographiques à émulsion compter le nombre de delta ray d’un tracé permet d’estimer le ratio Z²/v² de la particule ce qui permet de l’identifier, en complément d’autres méthodes comme le comptage de grain, la mesure de la portée ou la diffusion du tracé.
Probabilité de création de delta ray en fonction de la nature de la particule
B. Rossi dans High Energy Particles, 1952, explicite les probabilités de collision d’électrons et de particules lourdes sur des électrons atomique.
On défini Φcol(E,E’)dE’ comme la probabilité pour une particule chargée d’énergie E de transférer une énergie entre E’ et E’+dE’ à un électron atomique (production de delta ray).
Pour un électron incident d’énergie E et relativiste (β=1), Møller donne :
où Z et A correspondent à la charge et au numéro atomique du milieu traversé par la particule. La collision électron-électron atomique se faisant entre deux particules indiscernable, il faut interpréter cette équation comme la probabilité d’avoir un électron d’énergie E’ et l’autre à une énergie E-E’, avec E’ variant de 0 à E/2.
Pour une particule de masse m et de spin 1/2 (proton, muon), Bhabha, Massey et Corben donnent :
avec E’m l’énergie maximum transférable à un électron lors d’une collision frontale (« head on ») par une particule incidente relativiste donnée par :
où p correspond à la quantité de mouvement de la particule incidente et m sa masse. E’m correspond à wmax explicité en haut de la page avec E’m = wmax .
Une référence précise pour les particules lourdes : (avec E’m=>T‘max)
For delta rays production :
Pour la valeur de T‘max voir cette page (dernier calcul).
En résumé :
- Les particules (électrons, muons, protons, alphas) les plus lentes et les plus chargées créent le plus de deltas ray,
- les énergies maximum transférables aux électrons par des particules lourdes (muons, protons, alphas) sont faibles par rapport à un électron incident (jusqu’à la moitié de son énergie !), et au maximum égal à wmax = 2mev², (Nota : en mesurant la longueur d’un δray provenant d’une particule lourde on peut estimer grâce au tableau 4.2 l’ordre de grandeur de l’énergie de la particule incidente, en considérant que le delta ray est émis avec une énergie wmax.
- les deltas rays les plus probable sont ceux dont l’énergie est petite par rapport à wmax . Ces δrays sont émis préférentiellement à de larges angles (max : π/2) par rapport à la direction de la particule incidente.