We have this formula of scattering which is the probability that a charged particle of z,mp,v traversing a thickness of medium undergoes a collision which deflects the trajectory of the particle into the solid angle dw about θ from its original direction.
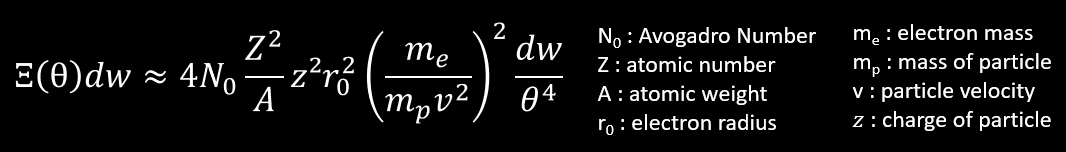
So to simplify, let’s assume that Ξ∼(1/mpv²)
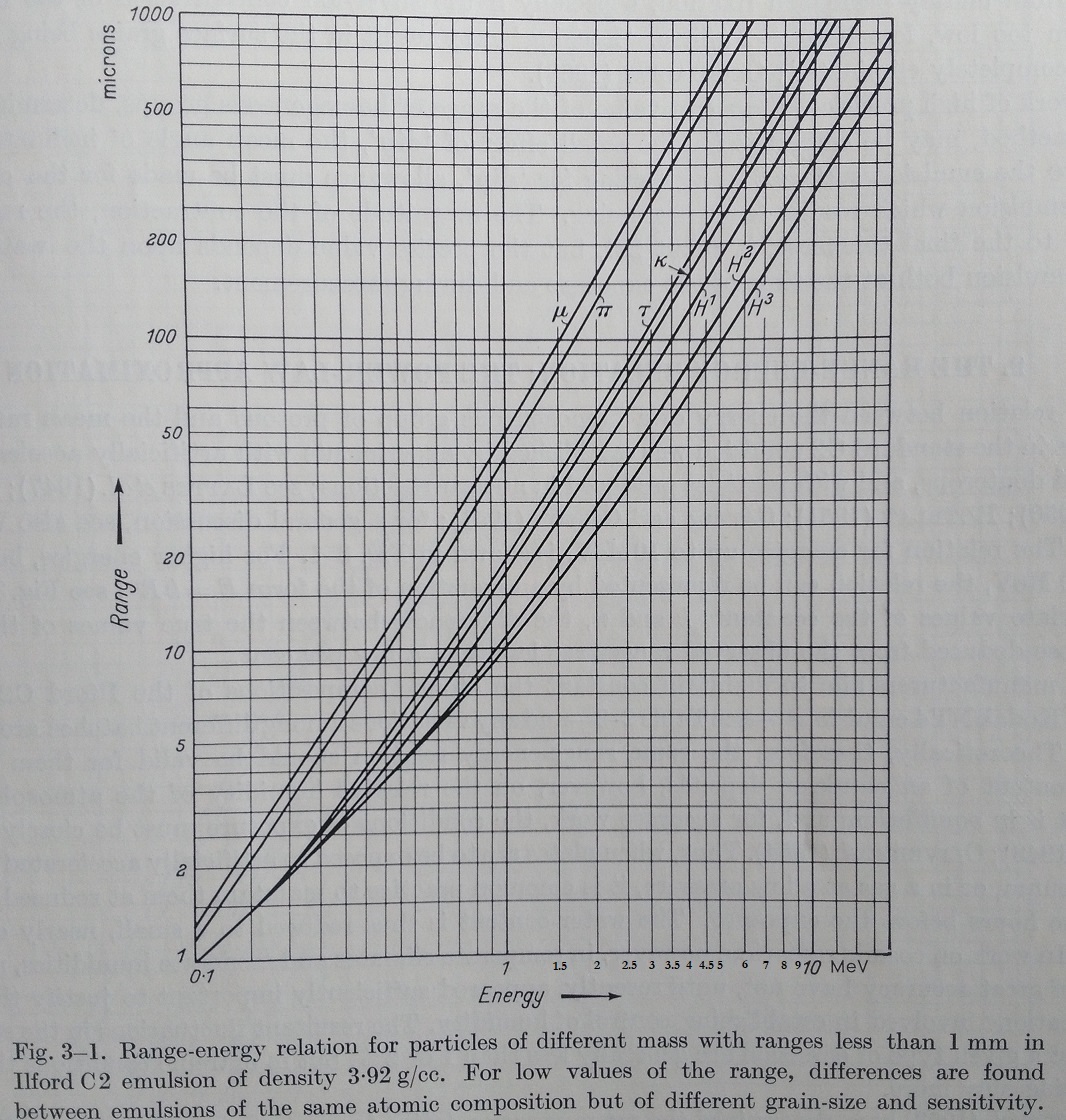
We have the energy range of particle in emulsion given by Powell :
We are considering the muon to proton particle below, which have about 200 μm of range in a photographic emulsion :
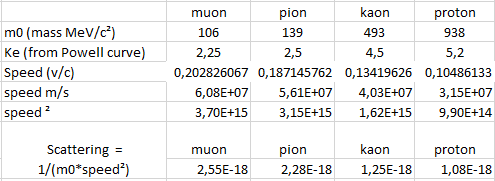
So for each particle and for 200 μm of range, we get the following kinetic energy of the particle :
We can use an useful excel sheet and get the speed for each particle from Ke and m0 :
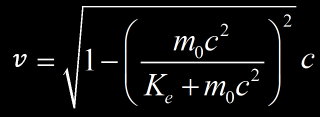
Next we can estimate the average scattering for each particle in the observed range with the top formula : Ξ∼(1/mpv²)
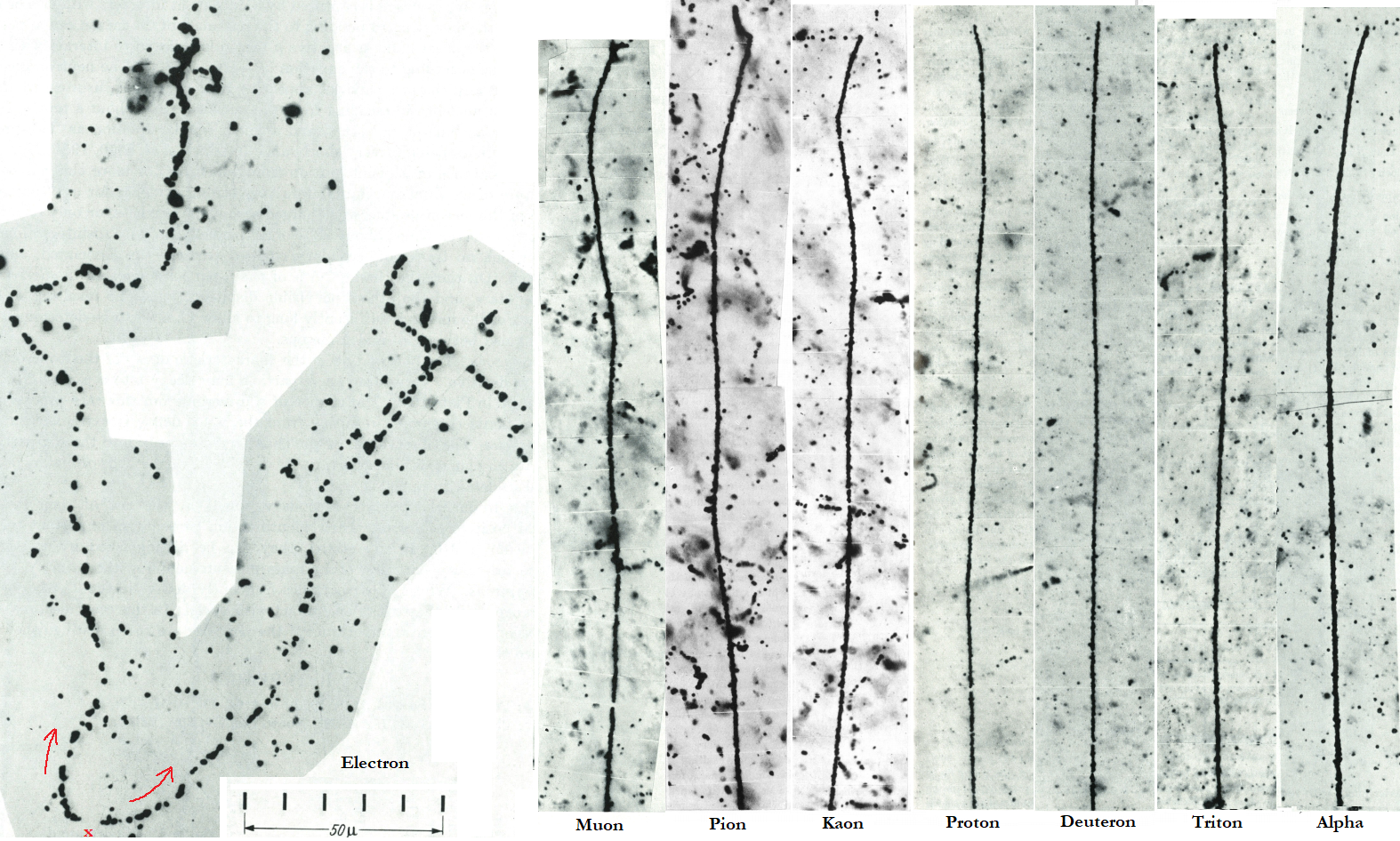
So the heavy particle (proton or kaon), expect less scattering than lighter particle (muon, pion). That we saw in the photographic emulsion. This is of course a coarse demonstration but show the importance of contribution of mass in the scattering. Even if the proton is 2x slower than a muon, it’s 9 times heavier. So even if the scattering depend of the square of velocity, this is not enough versus the huge difference of mass !
I don’t choose alpha particle because it’s charged twice so the scattering would be squared and we won’t be able to compare it with single charged particle. Electron are excluded too because they expect bremsstrahlung which false the range (muon and other heavy particle don’t lose energy with this process).