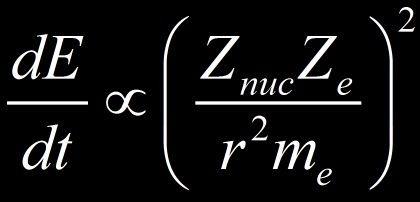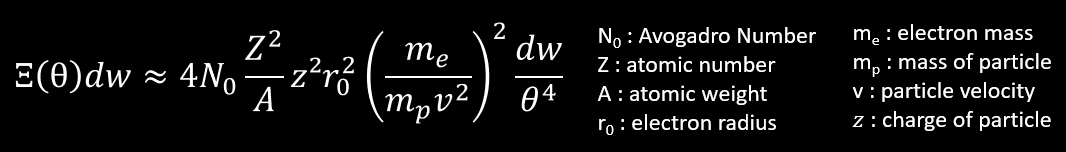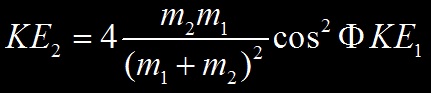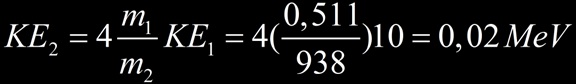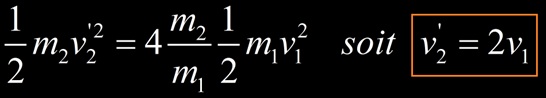Description of the energy losses process of an charged particle
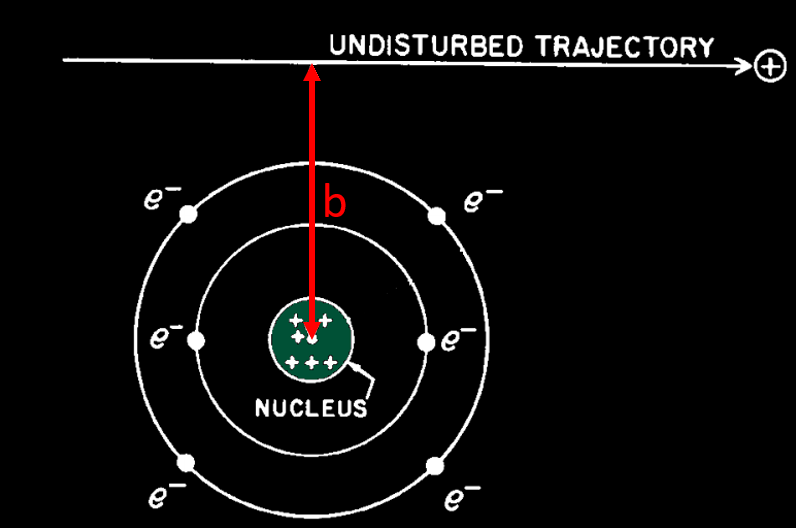
The energy loss of a charged particle travelling in matter come from two interaction process : by collision and radiative process. The probability of each process is determined by the distance of approach of the particle to the atom with which it interacts. This distance is called the impact parameter b.
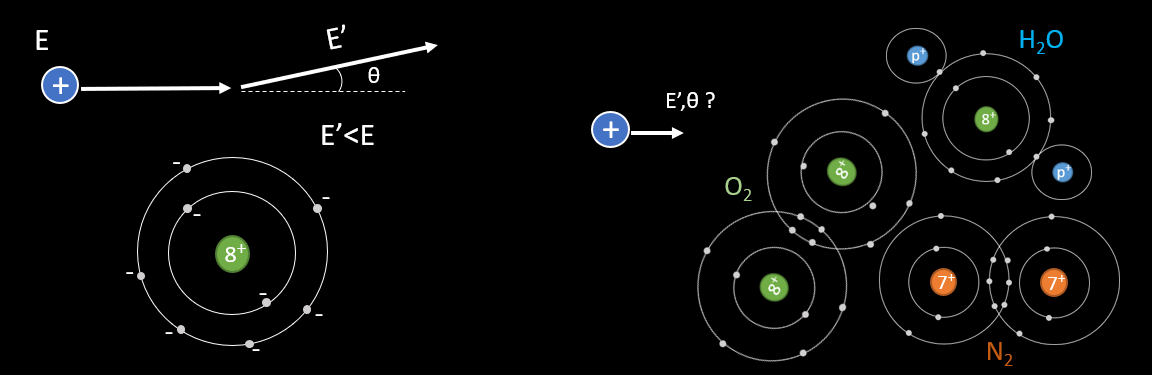
Collision process : If the distance of closest approach is large compared with atomic dimensions (b high), the atom as a whole reacts to the field of the passing particle. The result is an excitation or ionization of the atom (this ejected electron have almost no kinetic energy). If the distance of closest approach is of the order of atomic dimensions, the interaction is between the moving charged particle and one of the atomic electrons. This process results in the ejection of an electron from the atom with considerable energy. The ejected electron is called a « delta ray » and can make his own path in matter (minimum energy is about 100 eV). What we call collision is in fact an approximation as there is no physical collision between the incoming particle and the target particle (one electron of the atom, or a nucleus). All collision are « electrostatic » and made at various distance, according to the impact parameter. This is not the case during a nuclear reaction where the incoming particle is physically absorbed by the nucleus (but this is so rare that you will never see that in a common cloud chamber).
Electrostatic « collision ». As b get lower, the deflection of the incoming particle is higher and also the energy loss by radiation
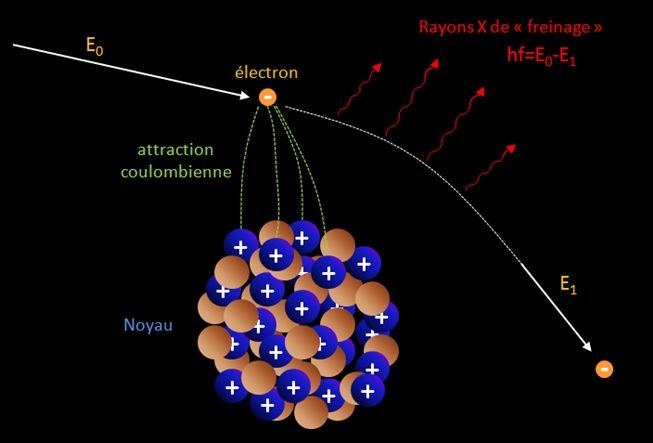
Radiative process : When the distance of closest approach becomes smaller than the atomic radius, the deflection of the particle trajectory in the electric field of the nucleus is the most important effect. This deflection process results in radiative energy losses and the emitted radiation (bremsstrahlung) covers the entire energy spectrum up to the maximum kinetic energy of the charged particle. But this radiative process is less frequent than the collision process because particle have much more chance to pass far from a nucleus than near to it.
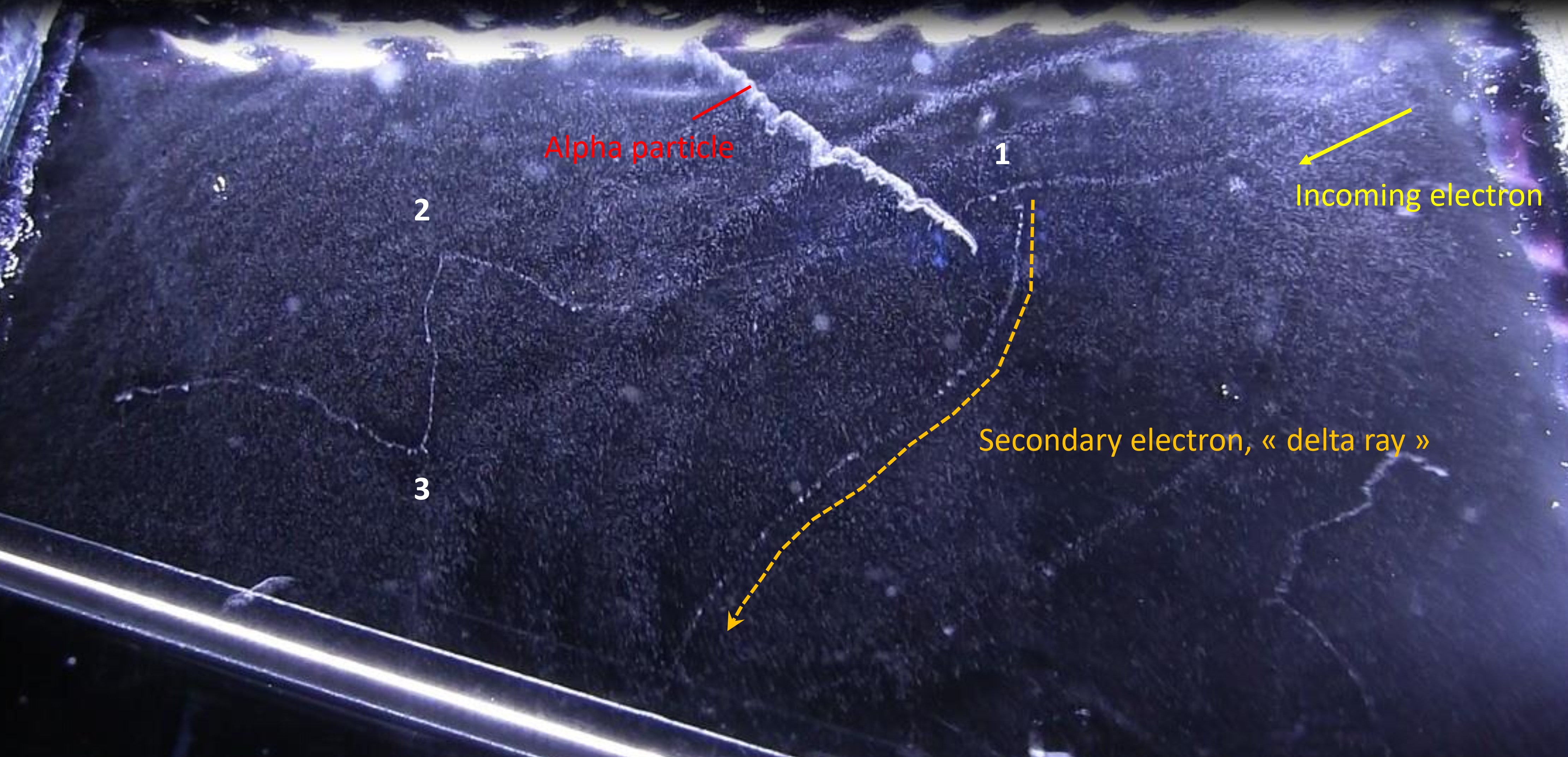
We can illustrate this 2 process of energy loss with a common cloud chamber picture.
In a cloud chamber picture, we see thousands of droplets building the path of the particle. Theses droplets come from the ions left by the particle travelling in matter, which ionized and excited the atoms. Producing ions require energy, so it’s a loss for the incoming particle. This is the first energy loss process due to the electrostatic « collision » of the incoming particle with the atom.
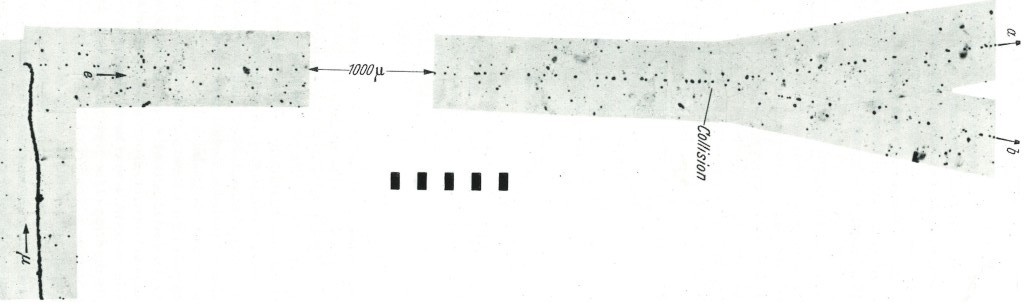
You can see the result of this energy loss in the next picture, with all the droplets making paths of particles travelling in the cloud chamber. The thin trails, composed of few droplets are electrons, whereas the fat brilliant trail in up-middle is made of much more droplets than the electrons. From the density of droplets (resulting in a track of high brightness ) we can say that it’s an alpha particle. So we can recognize which particle come in the chamber, just by looking at the density of tracks. The more ionization in matter => the more ions => the more energy loss of the incoming particle. As the energy loss trough the path of each particle (alpha, electron, proton…) is determined, we can identify it by looking at the quantity of droplets which is proportional to the brightness of the track.
Let’s analyse this picture further. An electron is coming from the up-right and travelling to left. Near the alpha track in up-middle of the picture, in point « 1« , we see a second track going to the bottom of the picture. This track has been created by the incoming electron. In this point, the distance of closest approach of the incoming electron is of the order of atomic dimensions : it results in a strong ionization of the atom with the ejection of one of it’s electron. This electron (called a « delta ray ») get a considerable kinetic energy from the incoming particle, enough to travel a long distance in matter and thus make his own track in a cloud chamber.
In the left of the picture, we see that the incoming electron make abrupt deviations (at point 2 and 3). This time, the particle went closer to a nucleus (impact parameter b low) and undergone a huge deflection by the electrostatic field of this nucleus. During this deflection, the incoming particle losses a high amount of energy by emitting X-rays (Bremsstrahlung). We can’t see the radiation emitted in the cloud chamber because X-rays are not charged particles and thus can’t create ions (but we can see the indirect X-rays interaction, like the tritium experiment). With this picture, we can determine the probability of occurrence between the collision and radiative process. At point 2 and 3, the huge deflection of the incoming particle show that there was 2 radiative process. If we count the number of droplet created along the path of the incoming electron, we will find about thousands (in fact this is the number of ions created by the particle). So the collision process is thousands time more probable than the radiative one, the latter involving small impact parameter.
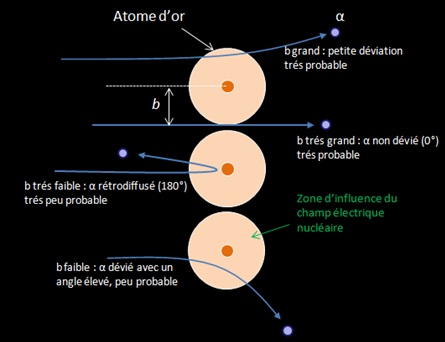
L’expérience de Rutherford (1909) peut montrer la prépondérance entre les deux processus de perte d’énergie pour une particule chargée traversant la matière. Dans une enceinte tirée au vide, il positionna une feuille d’or qui était bombardée par un faisceau de particule alpha collimaté. Les particules alpha provenant du Rn 222 ayant traversée la feuille étaient détectées spatialement avec un microscope muni d’un écran fluorescent en ZnS. Ainsi il pouvait mesurer l’angle de diffusion de la particule par rapport à sa trajectoire incidente.
La quasi-totalité des particules étaient détectées sous de faibles angles. Cependant, 1 particule α sur 10.000 était détectée à 90°, et certaines à plus de 150° : « It was as incredible as if you fired a 15 inch shell at a piece of tissue paper and it came back at you ». Seul un champ électrostatique intense pouvait dévier une particule alpha aussi fortement, ce qui prouva que les atomes sont constitués d’un « noyau » où était localisée toute la charge électrique. Rutherford proposa le modèle nucléaire de l’atome en 1911 suite à ces observations.
La courbe ci-dessous issue de l’expérience de Rutherford donne la probabilité de détection des particules alpha suivant l’angle de diffusion après que celles-ci aient traversées une feuille d’or de quelques μm d’épaisseur (ce qui correspond à une épaisseur de quelques milliers d’atome d’or).
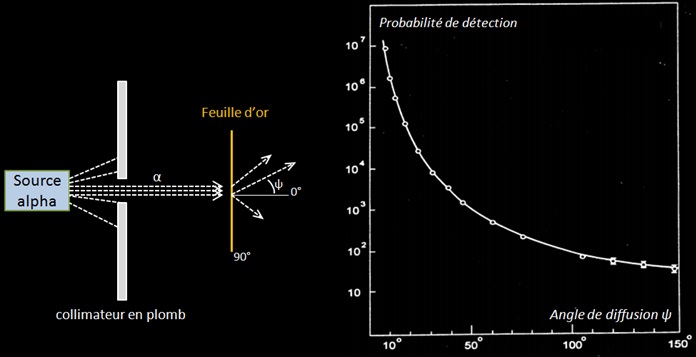
Expérience de Rutherford. La courbe montre la probabilité de détection (unité arbitraire) par rapport à l’angle de diffusion. Comme les particules alpha du Rn 222 ont une portée de quelques cm dans l’air l’expérience était réalisée dans le vide pour avoir un plus grand parcours des particules.
La courbe et l’équation de Rutherford montrent que la diffusion des particules sur des noyaux se fait majoritairement sous de faible angles. Ces faibles angles correspondent à des paramètres d’impact élevés où la particule passe loin du noyau. En effet étant donné la structure lacunaire de la matière, un faisceau de particules alpha à beaucoup plus de chance de passer « loin » du noyau (b grand) que de passer près de celui-ci.
Quelques particule ont donné de trés larges angles de diffusions. Ces particules sont passés prés du noyau sous de faibles paramètres d’impact, la particule étant déviée fortement par le champ électrostatique intense du noyau.
This experience show again that interaction involving low impact parameter, and thus the radiative process, are scarce.
Energy loss by radiative process
Lorsqu’un électron se rapproche d’un noyau la force d’attraction Coulombienne F=Z1Z2/4πε0r² augmente et la particule est déviée de sa trajectoire suivant la valeur du paramètre d’impact. Lors de cette « collision » l’énergie du système et la quantité de mouvement doivent se conserver. Or la déviation seule de l’électron ne permet pas de conserver le momentum (on a p0≠p1 soit mv0≠mv1 car v0≠v1 il manque ainsi une quantité pour avoir p0=p1). L’électron au cours de son accélération (qui est une variation de sa vitesse, ici diminuant) émet un spectre de rayonnements X (des photons) pour rétablir la conservation de la quantité de mouvement totale (pphoton = hf/c où f est la fréquence du photon).
La puissance rayonnée dE/dt par un particule chargée avec l’accélération a découle de la formule de Larmor :
Si l’on considère un électron s’approchant d’un noyau il est soumis à la force électrique et son accélération vaut :
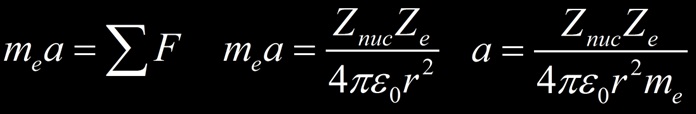
La puissance rayonnée par l’électron en rayonnement de freinage (Bremsstrahlung) est ainsi proportionnel à :
Nous avons considéré un électron me dévié par un noyau mais il pourrait s’agir de toutes autres particules chargées. D’après la formule on constate que :
- la perte par Bremsstrahlung est proportionnelle à la charge au carré des noyaux du milieu et de la charge de la particule (les tubes à rayons X utilise un faisceau d’électron avec une cible de noyaux lourd comme le Tungsten (Z=76) ).
- la perte par Bremsstrahlung est inversement proportionnel à la masse au carré de la particule (plus celle-ci est légère plus elle est susceptible de dévier et donc de rayonner).
- Plus la particule est proche d’un noyau (r), plus l’accélération est importante (ainsi que la déviation) et plus les pertes radiatives sont importante (dépendance en 1/r4)
Les particules lourdes seront peu soumises au rayonnement de freinage du fait de leur masse élevée : un muon est 207 fois plus lourd qu’un électron et perd ainsi 40.000 fois moins d’énergie par Bremsstrahlung qu’un électron. So radiative process are only for low mass particles such as electrons and positons.
Energy loss and scattering by collision process
We saw previously that low impact parameter involve radiative process, and that’s a relatively rare occurrence versus the collision process. This latter process involve high impact parameter, that’s to say the charged particle traversing a material medium will pass far from a nucleus, but not too far from the atom. Matter is made of atoms, which is composed of electrons and nuclei. If a charged particle pass nearby an atom, it will transfer energy and momentum to the closer electron and nucleus. During this exchange, the charged particle will be scattered, or deflected of a very small quantity θ from it’s initial direction of travelling.
The aim of this topic is to identifiate what are the quantity of energy loss and angle of scattering undergone by the incoming particle, to an electron or a nucleus. The problem will be studied with 1 atom of oxygen (see next picture). But in a cloud chamber the volume is made of many atoms of different structure : H2O, O2, N2, alcohol molecule… and so the particle will interact multiple time with this matter.
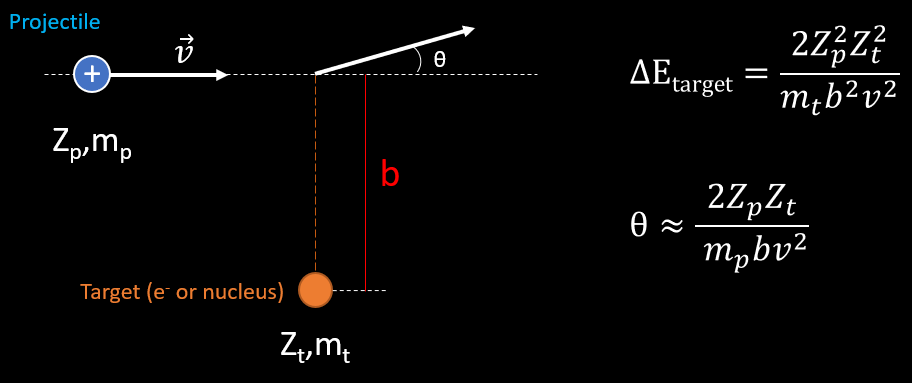
The problem can be studied in a simpler manner with application of electromagnetism (picture below). Consider that the projectile is non relativist heavy particle with mass mp and charge Zp whose initial velocity in the laboratory reference frame is v. In this frame, the scattering material is at rest : it can be an electron or a nucleus. We define the impact parameter b as the minimum traversal distance between the projectile’s initial direction of movement and the target position. The classical energy transfer to the atomic electron is defined with ΔE. The scattering angle of the projectile is θ.
The energy transfer is proportional to the square of the charge of the target particle and inversely proportional to its mass. Possible targets are electrons and nuclei. A nucleus has a larger charge than an electron by a factor of the atomic number Z, giving the nucleus an « advantage » by a factor of Z2 when it comes to extracting energy from the incident particle. However, nuclei are more massive than electrons by a factor of 1836A where A is the atomic weight which is as large as or larger than Z (mass of neutrons). Furthermore, there are Z more electrons than nuclei to act as targets. Hence we see that the electrons are more effective than nuclei at taking the energy of the incident particle by a factor of at least 1836. For this reason, we shall henceforth keep in mind that most of energy is lost by the incoming particle to the electrons of atoms because nucleus get thousands time less energy than one electron.
However, if we look at the scattering formula, things change. θ is directly proportional to the charge of the target if we consider the same value of b for one electron or nucleus as a target. If the target is an electron, Zt=e (e= elementary charge). If the target is a nucleus, θ ≈Ze. For example, if the nucleus is oxygen, the angle of scattering of the incoming particle will be 8 times than the angle of scattering induced by an electron. The angle of scattering is even smaller as the mass of the incoming particle is heavier. Thus, scattering of the projectile by atomic electrons can be neglected over the scattering induced by nuclei.
The next no-approximated formula of scattering is the probability that a charged particle of z,mp,v traversing a thickness of medium undergoes a collision which deflects the trajectory of the particle into the solid angle dw about θ from its original direction.
This formula (slighty simplified) tell that the probability of scattering at large angle is very small, but increase with the Z2 of the medium and z² of particle. If the particle is lighter and its velocity is low, the probability of scattering at large angle increase, but not at the same rate of the probability of scattering at small angles. Thus, when a particle lose more and more energy by collision with atomic electrons, the particle is more and more scattered by nuclei, we call this « multiple scattering« . If we look at the equation of the scattering probability in the field of atomic electron we will see that their contribution to scattering is fairly small (10% for Z = 10, 1% for Z = 82) even if their collisions are responsible for almost all of the energy loss of the incoming particle.
so a path ill not be perfeclty straight
So, when a charged particle penetrates an absorbing medium, most of the scattering interactions lead to very small deflections induced by the nuclei. Large net deflections are the result of a single large-angle scatter to a nucleus with a low impact parameter, but are statistically scarce.
two things happen: a) the particle loses energy traversing matter and b) particle is deflected from its initial direction • two main processes cause this: 1) inelastic collisions with atomic electrons in the material and 2) elastic scattering off nuclei • other processes also cause energy loss: 3) bremsstrahlung, 4) emission of Cherenkov radiation (relative of bremsstrahlung), 5) nuclear reactions (rare, lower probability) • makes sense to separate the consideration of heavy charged particles and light charged particles (i.e. electrons) • heavy particles don’t undergo 3) and 4); 5) is rare; 2) is again less common compared to 1)…and heavy particles don’t deflect much off electrons • basically need only consider inelastic collision with atomic electrons for energy loss of heavy charged particles
In a collision with a nucleus the proton will lose little energy, but its direction can
be changed completely; it can even bounce backwards. In collisions with electrons,
on the other hand, a large amount of energy can be transferred to the electrons, but
the direction of the proton can only be slightly changed. Indeed, there is a maximum
possible kinematical angle of deviation in such collisions. It needs a relativistic calculation to derive this angle. As a result, most of the energy loss of the proton is due
to the collisions with the electrons, and most of the change of direction is due to the
collisions with the nuclei.
Energy transfer and angle in elastic scattering with non-head-on collision (b≠0)
Précédemment nous avons décrit les transferts d’énergies des collisions électrostatiques de particules incidentes lourdes sur des électrons atomiques ou des noyaux. De nombreuses interactions observées dans une chambre à brouillard peuvent être expliquées par une approche mécanique des collisions c’est-à-dire en négligeant les interactions à distance des particules entre elles (leurs charges deviennent nulle). Cela revient à traiter ces collisions d’une manière classique avec des chocs réel entre les particules où seules les masses et vitesses entrent en compte. Bien que cette approche soit éloignée de la réalité, elle permet d’estimer simplement les quantités d’énergies échangées lors des chocs entre particules. Dans ce qui suit on négligera les énergies de liaison des électrons aux atomes, la force électrique, et on considérera que la vitesse du projectile est non relativiste.
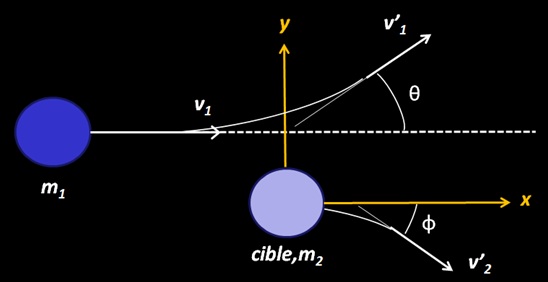
La collision à lieu entre un projectile de masse et de vitesse m1,v1 sur une cible immobile de masse m2. Il existe deux angles de diffusion : un angle θ pour le projectile et un angle Φ pour la cible. Le paramètre d’impact correspond à y ≠ 0 (la particule 1 percute la cible sur le bord)
L’énergie cinétique KE2 transférée du projectile à la cible se détermine à partir des lois de conservation de l’énergie cinétique et du momentum dont le détail figure ici. On obtient :
Où KE2 est l’énergie cinétique de la particule cible et KE1 l’énergie cinétique initiale de la particule projectile.
Angle of scattering from the values of m1 and m2 : A partir de l’équation précédente suivant la masse des entités en jeu nous pouvons identifier 3 cas of scattering.
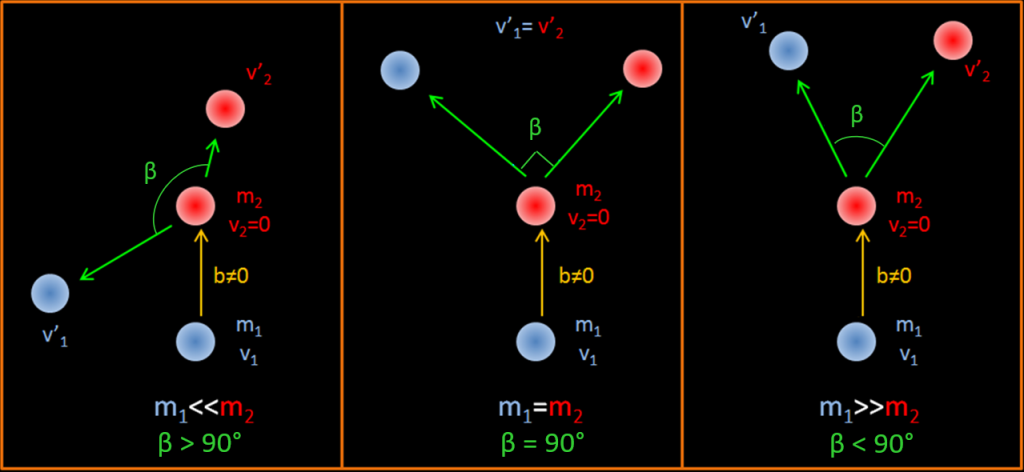
b≠0 signifie que la particule incidente percute la cible légèrement sur le bord et pas dans l’axe de la particule cible comme le montre le schéma.
The maximum energy transfer to the projectile occurs when the masses are equal. Si m1=m2, β=θ+Φ=90° et on peut montrer que KE2=KE1/2.
Observation of these 3 cases in a cloud chamber
m1 << m2
[Picture from 1936] An incoming electron (m1) coming from left, undergone a collision which scattered it at very large angle, almost 120° from its initial direction). This collision was due to a massive target, a nucleus (m2) under a small impact parameter. As the nucleus is massive (1836A time the electron), the electron didn’t transfer appreciable energy to the nucleus during the collision (refer to ΔE equation), but it lose a great quantity of energy by Bremssthralung. We can see that for m1<<m2, that the resulting angle of collision is higher than 90°. As the nucleus obtained no energy during the collision, we can’t see the recoiling nucleus.
There is a magnetic field about 300 Gauss in the chamber. Before the collision, the electron have to much energy to be deflected by this magnetic field. After collision, the electron have much less energy than before : it’s sensible to the magnetic field and thus start to make a spiral in the chamber. Near the end of its range, this electron undergo a second collision with a nucleus and is again deflected within a high angle, losing its last energy into Bremssthralung.
m1 >> m2
In the case of a collision of two equal rest mass particle(m0,1=m0,2 0 stand for « rest »), if one of them is at rest (m2=m0,2) and the other is moving at relativistic speed, m1=γm0,1. Thus, m1>>m2 and the subsequent direction of motion of the two particles is β<90°. Example below with a photographic emulsion of a muon (at left, moving upward) decaying into an electron. This electron moves right and have a kinetic energy about a dozen MeV from the μ decay process, its speed is relativist (near c) so its mass is not its rest mass, but a relativistic mass γm0,1. A stationary electron (m2=m0,2) in the emulsion is then collisioned by the incident relativist electron. The angle θ between the 2 electrons is <90° because m1>>m2 even if they are the « same » particles.
Note : the ejected electron is called a delta ray. Another example.
m1 = m2
In this case, both particles evolving in a collision have the same mass. To have a collision, this imply that one particle is moving, but not at relativistic speed so its mass is the same as its rest mass. This table indicate at which speed we can consider that a particle is relativist. For a 17 keV electron, γ (the lorentz factor) is 1,033. If this moving electron scatter into a immobile electron, we can say that m1 ≈ m2 . This is not true at 80 keV, because γ = 1,15. For a proton at 31 MeV , γ=1,033. At 145 MeV, γ = 1,15.

Lorsque m1=m2,l’angle de séparation des particules après la collision est de 90°. On retrouve ce comportement dans les jeux de billard où les angles entre les boules après chaque choc (non frontaux, b≠0) sont proches de 90° (proche, car une partie de l’énergie est perdu dans les mouvements de rotation : les collisions ne sont pas parfaitement élastique).
We can observe this type of collision in a cloud chamber, if you are lucky enough when you study the natural background.
http://www.cloudylabs.fr/wp/wp-content/uploads/2019/09/old.jpg
Dans la chambre à brouillard on peut observer ce phénomène rare lorsqu’un proton secondaire d’origine cosmique collisionne avec un proton (noyau d’hydrogène) d’une molécule d’eau ou d’alcool ce qui résulte en un angle de 90° entre les deux particules.
Video of the event.
Un proton secondaire, crée localement au niveau de la mer à partir d’une particule d’origine cosmique, interagit dans la paroi en verre de la chambre et éjecte un ou plusieurs protons. Ces protons entrent dans la chambre (flèche jaune et rouge sur la photo). La densité d’ionisation indique qu’il ne s’agit pas de particules alpha. Ni d’électrons, la chambre étant soumis à un champ magnétique, ces derniers auraient été déviés. Il ne peut s’agir de muons car leur vitesse relativiste ne laisse que des traces faiblement ionisé . Il s’agit bien de protons de quelques MeV. L’un des deux protons (en rouge), collisionne avec un atome d’hydrogène contenu soit dans une molécule d’eau (H2O) ou d’alcool (C3H8O). Le proton incident étant de faible énergie (quelques dizaines de MeV tout au plus), on peut considérer que sa masse est égale à celle de repos (vitesse nulle), soit qu’elle est identique a la masse du proton du noyau d’hydrogène. Dans ce cas, la mécanique des collisions élastique indique que l’angle de déviation entre les deux particules doit être de 90°, emportant chacun la moitié de l’énergie cinétique du proton incident.
Ces différents cas de collision sont visibles dans la chambre à brouillard. Lorsqu’on injecte un gaz plus ou moins lourd dans la chambre les particules nucléaire collisionnant avec les atomes de gaz seront déviées sous des angles caractéristiques. Quelques images de diffusion de particule alpha sur des gaz.
Transfert d’énergie entre deux particules lors d’une collision élastique frontal (b=0)
On peut simplifier la formule précédente en considérant que les particules se rencontrent « frontalement » : dans ce cas cos²Φ =1 et les transferts d’énergies cinétique sont maximales.
Dans ce type de collision :
- le paramètre d’impact b=0 (choc « frontal » entre les deux particules)
- l’angle de diffusion de la cible vaut Φ=0
- l’angle de diffusion θ du projectile vaut soit 0 ou 180° dépendant de la valeur des masses m1 et m2 :
si m1>m2, θ = 0 si m1<m2, θ=180° et si m1=m2 le projectile s’arrête et la cible diffuse avec un angle Φ=0
L’énergie cinétique maximale qui peut être transférée à la cible s’écrit : 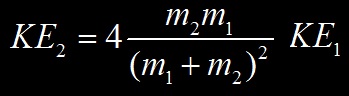
Plusieurs cas de figures sont possibles pour déterminer l’énergie cinétique KE2 gagné par la particule immobile.
- Si m1<<m2 exemple : un électron (m1=0,511 MeV/c²) percutant un noyau d’hydrogène (m2=938 MeV/c²), avec KE1 = 10 MeV
L’électron transfert très peu (0,2%) d’énergie cinétique au noyau (néanmoins il perdra de l’énergie sous forme de Bremsstrahlung exemple dans une chambre à brouillard). Si c’est une particule alpha qui diffuse sur un noyau d’or le rapport de masse montre que seulement 8% de l’énergie de la particule alpha incidente est cédée au noyau.
Autre exemple : si un neutron collisionne avec un noyau de plomb, 4*mn/mpb =0,02. Seul 2% de l’énergie cinétique du neutron est transféré au noyau de plomb. Cela montre que le plomb est très peu efficace pour ralentir les neutrons. Il faut privilégier des matériaux à faible numéro atomique comme le Bore, utilisé dans les réacteurs nucléaire comme modérateur neutronique (A=11, 4*mn/mB =0,36). Le plomb n’est efficace que pour atténuer les rayonnements électromagnétique sensible aux matériaux de haute densité.
- Si m1>>m2 exemple : un proton (m1) percutant un électron atomique immobile (m2).
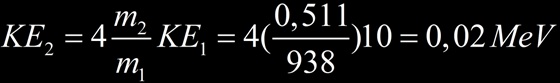 On retrouve le cas précédent le proton cède très peu d’énergie (0,2%) à l’électron immobile. Plus la masse du projectile est élevée et moins la cible recevra d’énergie. Dans l’exemple 20 keV d’énergie cinétique reçu par l’électron correspond à un parcours dans l’air de 8 mm. Toujours dans le cas m1>>m2 la vitesse de l’électron vaut :
On retrouve le cas précédent le proton cède très peu d’énergie (0,2%) à l’électron immobile. Plus la masse du projectile est élevée et moins la cible recevra d’énergie. Dans l’exemple 20 keV d’énergie cinétique reçu par l’électron correspond à un parcours dans l’air de 8 mm. Toujours dans le cas m1>>m2 la vitesse de l’électron vaut :
- Si m1=m2
![]()
Lorsque m1=m2 on distingue deux cas :
Le premier cas fait intervenir deux particules discernable c’est à dire que l’on peut reconnaître après le choc (par exemple en mesurant leur charge). C’est le cas pas exemple lorsqu’un positon (q=1) percute un électron immobile (q=-1), ou lorsqu’un neutron percute un noyau d’hydrogène (en considérant que mn=mp on distingue encore ces particules suivant leur charge). Le choc de deux particules discernable équivaut au « carreau de pétanque » : au choc, m1 s’immobilise et m2 part avec v1. Cliquer ici pour voir à quoi ressemble un « carreau de pétanque » entre un positon et un électron.
Le second cas fait intervenir deux particules indiscernable comme un électron percutant un autre électron atomique immobile. Le transfert d’énergie cinétique maximale lors du choc élastique de deux particules indiscernable vaut :
- KE2=KE1/2 dans le cas d’un choc non frontal, comme vu plus haut
- KE2=KE1 dans le cas d’un choc frontal, mais il est impossible de dire si il y a eu réellement collision car les particules sont indissociable.
Dans le cas m1=m2 il ne faut pas négliger les effets relativiste. Si la particule incidente est un électron avec une vitesse élevée il faut prendre en compte la valeur de sa masse inertielle qui est supérieur à celle de l’électron atomique au repos. Comme les masses de ces deux particules indiscernable sont en réalité différente le transfert d’énergie cinétique ne sera pas égale à KE2=KE1/2. On revient alors au cas m1>>m2 : ici la particule incidente devenu massive par sa vitesse, cède peu d’énergie à la cible. Après l’interaction on considère que l’électron ayant le plus d’énergie cinétique est la particule incidente. Exemple d’un tel cas dans une chambre à brouillard.
XYZ
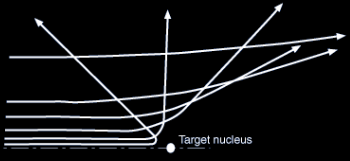
On retient de cette expérience qu’une particule traversant la matière subira des diffusions répétées à faible angles avec les noyaux atomiques, ce qui va petit à petit, modifier sa trajectoire comme illustrée ci-dessous.
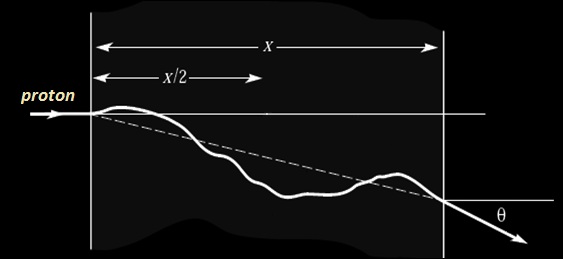
Trajectoire d’un proton traversant une épaisseur x de matière. Les déviations sont exagérés par rapport à la réalité.

On considère que les déviations des particules sont dues uniquement à des paramètres d’impact grand en négligeant les diffusions à larges angles beaucoup moins probable. En traitant le mécanisme de diffusion multiple sous de faible angle de manière statistique on peut calculer l’angle de diffusion moyen {θ} par rapport à la trajectoire initiale de la particule après que celle-ci ait traversée une épaisseur de matière déterminée.
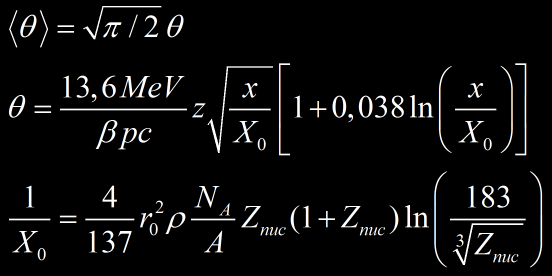
z est la charge de la particule, X0 la longueur de radiation et x l’épaisseur de matière traversée.
r0 est le rayon de l’électron, A la masse molaire du matériau, Znuc la charge du matériau, Na le nombre d’Avogadro et ρ sa masse volumique.
D’après l’équation on constate que plus l’épaisseur de la matière traversée est grande de même que sa densité, et plus la déviation sera importante. De même plus la particule est rapide et moins la déviation sera grande.
Un muon de momentum 4 GeV/c (β=0,999 et pc= 4000 MeV) diffusera avec un angle moyen de 10,8 mrad dans l’eau, 20 mrad dans le plomb (1,1°) et 26,9 mrad dans l’uranium, pour une épaisseur x=10 cm de matériau traversée.
Lorsque la particule incidente (autre qu’un électron) dispose de suffisamment d’énergie pour se rapprocher du noyau cible celui ci peut recevoir par l’intermédiaire de la force électrique une certaine quantité énergie qui peut servir à :
- exciter le noyau (collision inélastique),
- transférer de l’énergie cinétique au noyau (collision élastique). Sous l’impact (à distance) l’atome s’ionise et le noyau « recule » formant une trace très courte (quelques mm) dans la chambre à brouillard. L’atome ionisé récupère très rapidement des électrons du milieu ambiant pour conserver sa neutralité électrique. La perte d’énergie par collision inélastique du noyau est au minimum de (2 MeV.cm²/g) * (la densité du milieu en g/cm3)*(Z² du noyau) comme décrit par l’équation de Bethe.

Noyau de recul observé dans la chambre à brouillard. Une particule alpha émis par de l’Américium 241 à fait une collision élastique « non frontal » avec un noyau du milieu qui s’est déplacé sous l’impact électrostatique.
Si l’énergie de la particule alpha est suffisante (et si b=0) la particule alpha peut pénétrer le noyau et faire une réaction nucléaire. Blackett en 1925 fut le premier à capturer sur film photographique une transmutation d’un noyau d’azote en oxygène en utilisant des particules alpha du 212Po (Emax : 8.9 MeV) et du 212Bi (Emax : 6.2 MeV).
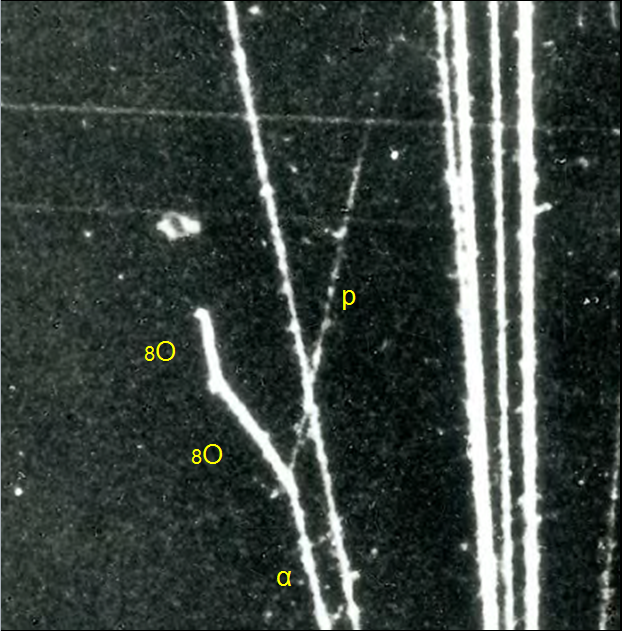
Les particules alpha viennent du bas. L’une d’elle à gauche percute physiquement un noyau d’azote de l’air. La particule alpha est capturée et le noyau devient un noyau de Fluor 18 excité et très instable. Ce noyau se désintègre aussitôt en Oxygène 17 émettant une particule qui laisse une trace faiblement ionisée caractéristique d’un proton. Le noyau d’oxygène à reculé sous l’impact de la particule alpha primaire et collisionne avec un autre noyau avant la fin de sa trajectoire (on peut observer une très petite trace vers la gauche lors du changement de direction du noyau d’oxygène). Le noyau capture peu à peu des électrons à mesure qu’il ralentit et devient neutre formant un atome d’oxygène 17 stable. La trace disparaît, dès la neutralité de l’atome atteinte. Un autre cliché.
Les énergies des particules alpha des isotopes naturels sont tout juste suffisante pour faire de telle réactions (il faut prendre en compte l’énergie perdu par la particule pendant son parcours avant qu’elle ne rencontre le noyau cible). Les transmutations sont des événements exceptionnel dans les chambres à brouillard : sur 23.000 photographies effectuées par Blackett entre 1921 et 1924 dans une chambre à expansion automatisée seul 8 photos ont montrées des cas de transmutation nucléaire avec des noyaux d’azote. Pour que cette réaction puisse se produire il faut que la particule alpha puisse vaincre la répulsion Coulombienne du noyau d’Azote ce qui est possible si l’énergie cinétique est au minimum de 4,99 MeV . Cependant une particule alpha à une probabilité non nulle de passer la barrière Coulombienne par effet tunnel : l’ énergie seuil de la réaction devient égale à 1,53 MeV).
La diffusion des électrons sur des noyaux est identique à celui des particules lourdes vue précédemment via l’expérience de Rutherford comme le montre la courbe ci dessous. Lorsqu’un électron passe loin d’un noyau les angles de diffusions sont faibles et cela représente une proportion élevée d’événements. A l’inverse, il est moins fréquent qu’un électron passe prés d’un noyau et soit détectée avec un angle de déviation large. Du fait de leur faible masse, un électron peut aussi être rétrodiffusé par un noyau (angle de diffusion 180°, sans perte d’énergie), propriété utilisée dans les microscopes électronique à balayage.
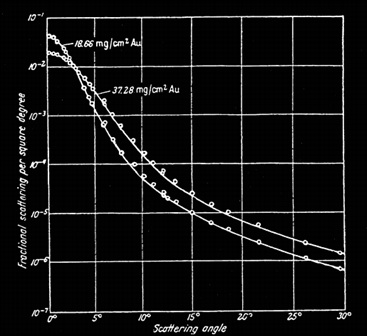
Distribution des angles de diffusion pour des électrons de 15,7 MeV traversant deux feuilles en or de différentes épaisseurs (18,66 mg.cm-2/19300 mg.cm-3=9,6μm ; 37,28 mg.cm-2/19300 mg.cm-3 =19,3μm). L’ordonnée donne la probabilité de détection. La feuille d’or la plus épaisse donne un peu plus d’événements car il y a plus de noyaux où les électrons peuvent diffuser. Les angles de diffusion élevés correspondent à des événements uniques de diffusion d’électron près des noyaux. Pour les angles de diffusion faible (<5°), les événements sont liés à des diffusions multiples éloigné des noyaux.
Lorsqu’un électron se rapproche d’un noyau la force d’attraction Coulombienne F=Z1Z2/4πε0r² augmente et la particule est déviée de sa trajectoire suivant la valeur du paramètre d’impact. Lors de cette « collision » l’énergie du système et la quantité de mouvement doivent se conserver. Or la déviation seule de l’électron ne permet pas de conserver le momentum (on a p0≠p1 soit mv0≠mv1 car v0≠v1 il manque ainsi une quantité pur avoir p0=p1). L’électron au cours de son accélération (qui est une variation de sa vitesse, ici diminuant) émet un spectre de rayonnements X (des photons) pour rétablir la conservation de la quantité de mouvement totale (pphoton = hf/c où f est la fréquence du photon).
La puissance rayonnée dE/dt par un particule chargée avec l’accélération a découle de la formule de Larmor :
Si l’on considère un électron s’approchant d’un noyau il est soumis à la force électrique et son accélération vaut :
La puissance rayonnée par l’électron en rayonnement de freinage (Bremsstrahlung) est ainsi proportionnel à :
Nous avons considéré un électron me dévié par un noyau mais il pourrait s’agir de toutes autres particules chargées. D’après la formule on constate que :
- la perte par Bremsstrahlung est proportionnelle à la charge au carré des noyaux du milieu et de la charge de la particule (les tubes à rayons X utilise un faisceau d’électron avec une cible de noyaux lourd comme le Tungsten (Z=76) pour produire des rayons X).
- la perte par Bremsstrahlung est inversement proportionnel à la masse au carré de la particule (plus celle-ci est légère plus elle est susceptible de dévier et donc de rayonner).
- Plus la particule est proche d’un noyau (r), plus l’accélération est importante (ainsi que la déviation) et plus les pertes radiatives sont importante (dépendance en 1/r4)
Les particules lourdes seront peu soumises au rayonnement de freinage du fait de leur masse élevée : un muon est 207 fois plus lourd qu’un électron et perd ainsi 40.000 fois moins d’énergie par Bremsstrahlung qu’un électron.
.
Résumé des processus de pertes d’énergies et de diffusions
- Les particules chargées traversant la matière interagissent à distance via la force électrique avec les noyaux et les électrons atomique qu’ils rencontrent. Les pertes d’énergie des particules se font essentiellement via les collisions inélastiques avec les électrons atomiques car l’on considère statistiquement qu’il y a plus d’électrons cibles que de noyaux cibles. Concernant la particule incidente plus elle est lente et chargée et plus elle cédera d’énergie aux électrons atomiques.
- Les particules lourdes (m>>melectron) ne diffusent (=dévient) que sur des noyaux et peuvent céder de l’énergie à ces derniers qui peuvent « reculer » en acquérant une fraction d’énergie cinétique. L’angle de diffusion augmente si la vitesse de la particule diminue (dépendance au carré), si la particule se rapproche du noyau ou si les charges projectile-cible sont élevées. Même si la collision inélastique entre une particule lourde et un électron atomique ne représente qu’une perte d’énergie infinitésimale pour la particule, les multiples collisions successives finiront par consommer l’intégralité de l’énergie de la particule. La perte d’énergie d’une particule lourde est un processus de perte continu décrit par l’équation de Bethe.
- Plus une particule est rapide et moins elle passe de temps près des champs électrostatiques (électrons, noyaux) qui pourrait influer sur sa trajectoire. Au début d’un tracé dans une chambre à brouillard l’énergie de la particule est élevée et la formule de Rutherford montre que seulement des diffusions multiples à faible angles sont probables. A la fin du tracé l’énergie cinétique est moindre et les diffusions sous de grands angles sont de plus en plus fréquentes. La valeur des angles de diffusion est inversement proportionnelle à la masse de la particule : l’électron très léger pourra être aisément dévié sous de larges angles par les noyaux. La diffusion multiple est proportionnelle à la densité et au numéro atomique du matériau traversé.
- Un δray (delta ray) est un électron issu de l’ionisation de l’atome lors de la collision inélastique d’une particule et d’un électron atomique. La vitesse maximale que peut acquérir un δray est de deux fois la vitesse de la particule incidente. Un δray dispose d’assez d’énergie pour réaliser des collisions inélastique avec d’autres électrons atomique créant d’autres paires d’ions agissant en tant que points de condensation ce qui constitue une trace dans la chambre à brouillard. Les δray sont éjectés à un angle maximum de 90° par rapport à la direction de la particule incidente (voir cette page pour plus de détails).
- Concernant les électrons : Le rapport de masse entre un noyau et un électron incident fait que l’énergie transférable au noyau cible lors de la collision est minime. On qualifie cette collision d’élastique : l’électron sera seulement dévié de sa trajectoire avec un angle de diffusion dépendant de son paramètre d’impact, de sa vitesse ou de la charge du noyau. Cependant, plus un électron est proche d’un noyau, plus la déviation est importante et plus les pertes d’énergie par Bremsstrahlung le sont. A faible énergie un électron sera facilement dévié de sa trajectoire par l’influence du champ électrostatique des électrons atomique (et des noyaux) ce qui résulte en une trajectoire en « zig zag ». Lors d’une collision inélastique avec un électron atomique, une importante quantité d’énergie peut être cédé à l’électron atomique (jusqu’à la totalité en cas de choc « frontal »). Le processus de perte d’énergie des électrons ne se fait donc pas de manière continu comme les particules lourdes mais de façon aléatoire ou discontinu.
- Un électron de haute énergie (> une centaine de keV) décrit une trajectoire rectiligne dans la chambre à brouillard mais cela « ne dure pas longtemps » : il suffit qu’il soit dévié une seule fois par un noyau sous un angle élevée pour perdre la majorité de son énergie par rayonnement de freinage. Un muon par rapport à un électron, est quasiment insoumis au Bremsstrahlung et ne perdra son énergie que de manière continu avec les électrons atomique. Sa trajectoire sera rectiligne comme toute celle des particules lourdes. Cependant il peut arriver qu’il passe prés d’un noyau et avoir sa trajectoire modifiée sous un angle important, bien que cela soit peu probable comme vue avec l’expérience de Rutherford.
- Dans le cas où l’une des deux particules est immobile avant une collision élastique les trois trajectoires (v1, v’1 et v2) sont contenus dans un seul plan (conservation vectorielle de la quantité de mouvement). Il suffit que la particule incidente soit dans le plan d’observation de la chambre à brouillard pour voir le projectile et la cible diffusée (schéma ci dessous).
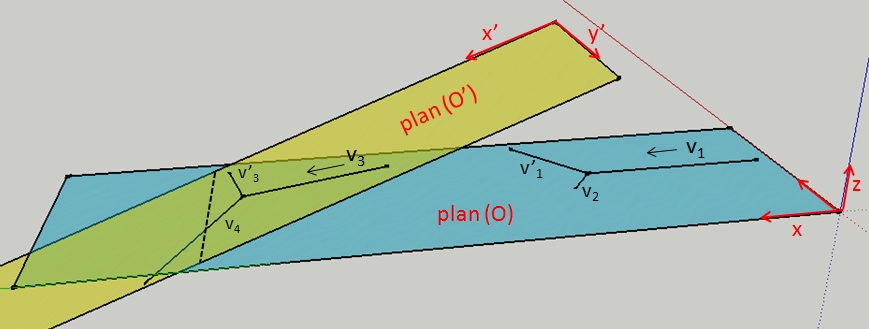
Collision élastique dans deux plans. Le plan O correspond au plan d’interaction de la chambre à brouillard, le plan O’ traverse le plan O. Dans le cas d’une collision où la cible est immobile, les directions des particules résultant du choc sont contenus dans le même plan que celui de la particule incidente. Pour voir la collision dans la machine, il faut que la particule incidente soit contenu dans le plan de visualisation de la chambre (ce qui est le cas avec une particule de direction et vitesse V1 mais pas pour V3).